Угол при вершине равнобедренного треугольника равен 96градусов. Найдите острый угол, под которым пересекаются биссектрисы углов при основании треугольника.
СРОЧНООООООООООООООООООООООООООООООООООО !!!!!!!!!!!!!!!!!!!!!!
Аноним:
пж быстрее срочно нуужно
с решением ответом)
и ответом*
пжпжпжпжпжпжпжжпжппжпжпжпжпж быстреееееееееееееееее
Ответы
Ответ дал:
2
Ответ:
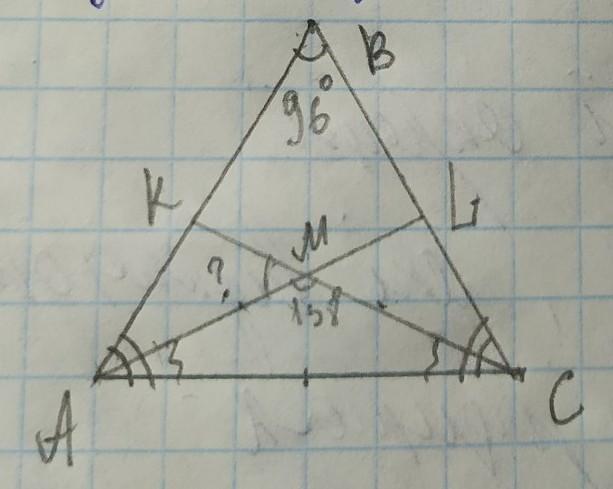
∆ABC- рівнобедрений AB=BC CK і AL- бісектриси
кут A=куту C- як кути при основі рівнобедреного трикутника 180°-96°=84° 84°÷2=42° кут A=куту C=42°
кут MAC=21°- за властивістю бісектриси,
кут MCA=21°- за властивістю бісектриси, ∆AMC- рівнобедрений, зовнішній кут дорівнює сумі двох внутрішніх не суміжних з ним, кут AMK=21°+21°=42°
Приложения:
извини но яне понимаю украинский язык)))
ΔABC- равнобедренный AB = BC CK и AL- биссектрисы
угол A = углу C- как углы при основании равнобедренного треугольника 180 ° -96 ° = 84 ° 84 ° ÷ 2 = 42 ° угол A = углу C = 42 °
угол MAC = 21 ° - по свойству биссектрисы,
угол MCA = 21 ° - по свойству биссектрисы, ΔAMC- равнобедренный, внешний угол равен сумме двух внутренних НЕ смежных с ним угол AMK = 21 ° + 21 ° = 42 °
угол A = углу C- как углы при основании равнобедренного треугольника 180 ° -96 ° = 84 ° 84 ° ÷ 2 = 42 ° угол A = углу C = 42 °
угол MAC = 21 ° - по свойству биссектрисы,
угол MCA = 21 ° - по свойству биссектрисы, ΔAMC- равнобедренный, внешний угол равен сумме двух внутренних НЕ смежных с ним угол AMK = 21 ° + 21 ° = 42 °
нуу сори но я уже нашел решение но спасибо)))
ты пабг не играешь?) ахах тупой вопрос
нет
пххпх
а жаль ххаха
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад