Составьте уравнение производной к графику функции f в точке с абсциссой x0, если:
Приложения:
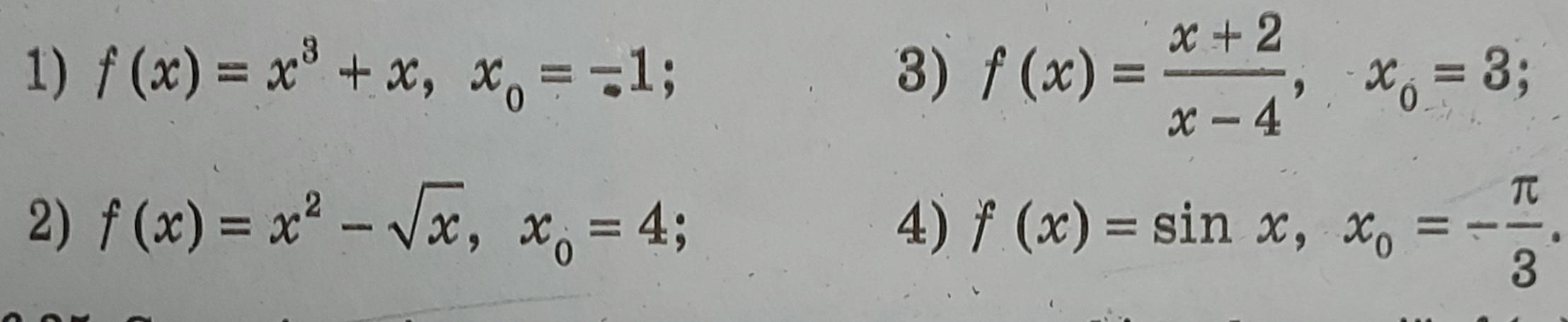
karolinka6:
может вам надо написать уравнение касательной к графику?
Др
Уравнение производной
Тогда может найти значение производной в точке Xo ?
Да
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад