Question

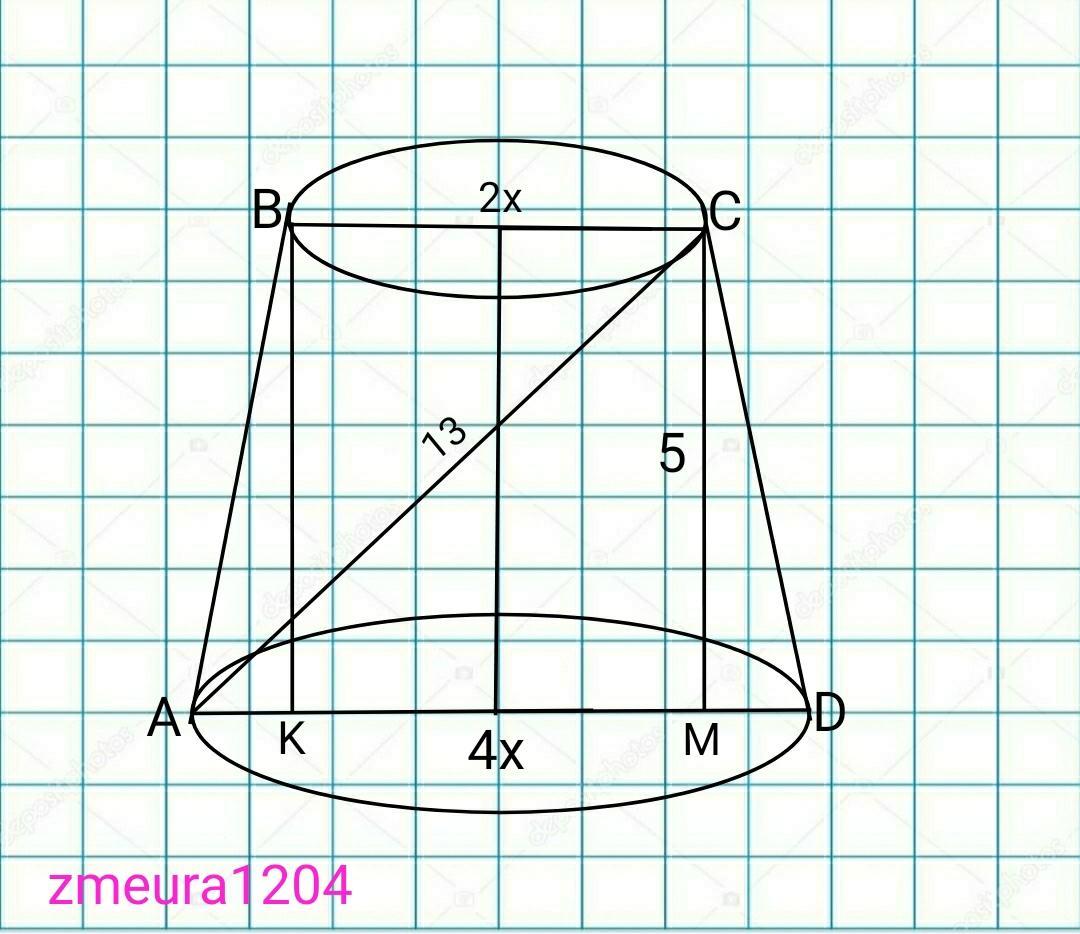
высота усечённого конуса равна 5, а диагональ осевого сечения -13. радиусы оснований относятся как 1:2 найдите площать боковой поверхности усечённого конуса, с рисунком пожалуйста ​

Answer 1

Ответ:

12π√41 ед²

Объяснение:

r:R=1:2

Тогда

d:D=2:4

Пусть диаметр ВС будет 2х; диаметр АD будет 4х.

АК=МD

AK=(AD-BC)/2=(4x-2x)/2=x

AM=AK+BC=x+2x=3x.

∆АСМ- прямоугольный треугольник

По теореме Пифагора

АМ=√(АС²-СМ²)=√(13²-5²)=√(169-25)=

=√144=12 ед.

3х=12

х=12/3

х=4.

АМ=МD=4.

BC=2x=2*4=8 диаметр верхнего основания.

АD=4x=4*4=16 диаметр нижнего основания.

r=BC/2=8/2=4

R=AD/2=16/2=8.

∆СМD- прямоугольный треугольник

По теореме Пифагора

СD=√(CM²+MD²)=√(5²+4²)=√(25+16)=

=√41 ед.

Sбок=π(R+r)*CD=π√41(8+4)=12π√41 ед²