Найти частное решение дифференциального уравнения,
которое удовлетворяет приведенным начальным условиям:
Приложения:
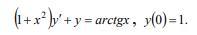
Ответы
Ответ дал:
2
Ответ:
Это линейное ДУ
По частям:
Получаем:
общее решение
частное решение
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад