Вершины треугольники делят описанную около него окружность на три дуги, длины которых относятся как 6:9:21. Найдите радиус окружности, если меньшая из сторон треугольника равна 12.
Simba2017:
углы треугольника вписанные, равны половинам дуг, на которые опираются
найдете дуги и углы, а там т синусов
)))))
Дорогие математики! Есть задачка знания.ком/таск/44620442. Помогите ребенку! На черновике сделала, но все красиво начертить нет сил сейчас))
Ответы
Ответ дал:
2
Ответ:
решение на фотографии.
Приложения:
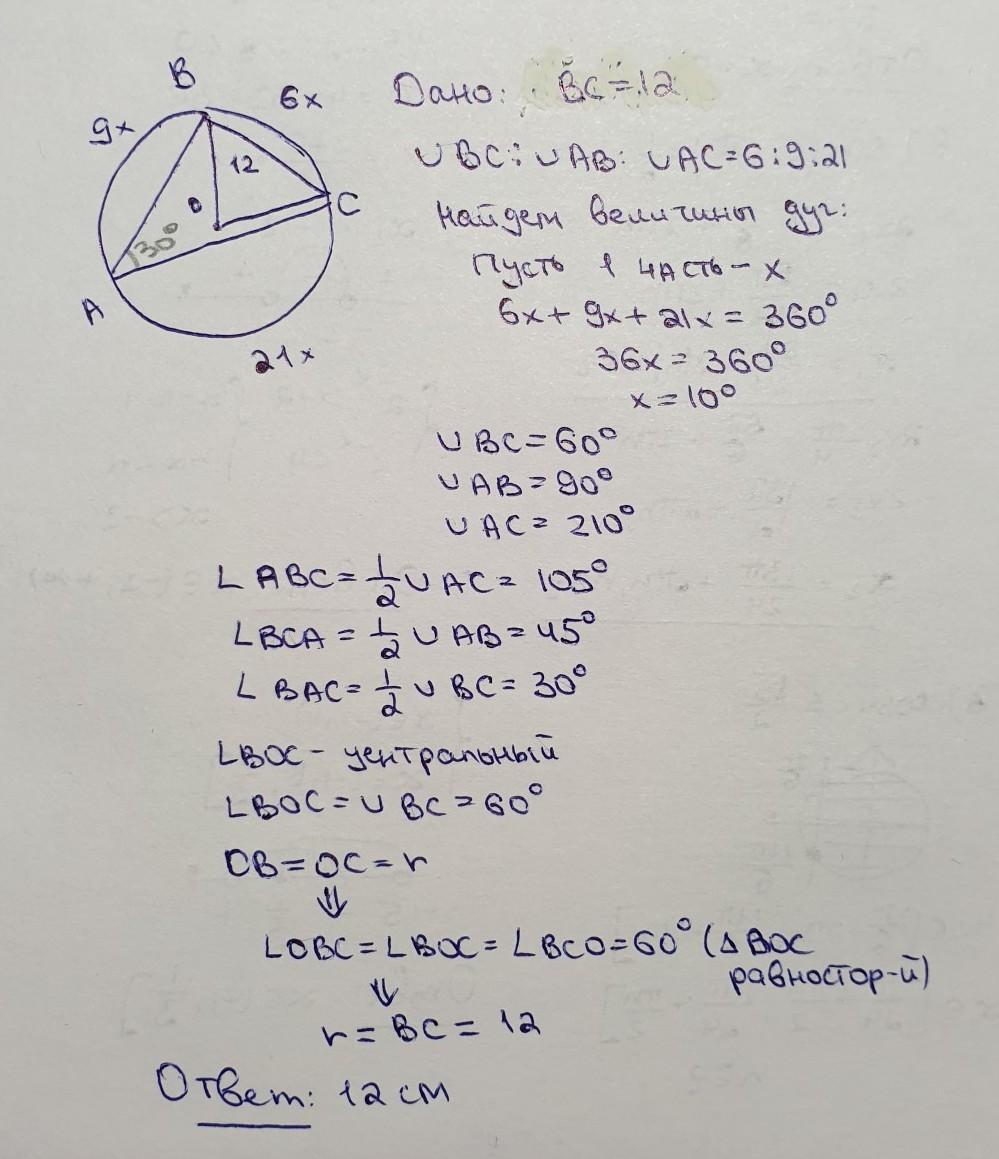
Ответ дал:
3
Пусть коэффициент пропорциональности х, х>0, тогда
6х+9х+21х=360, откуда х=360/36=10
Меньшая из дуг равна 6*10°=60°, на нее опирается меньший из вписанных углов, который равен половине дуги 60°, т.е. меньший из улов треугольника равен 60°/2=30° , а по следствию из теоремы синусов
а/sin30°=2*R⇒R=12/(2*0.5)=12
Ответ 12
ты гавно вареное, из за тебя мой акк удалили я блть ученым был ска
павтарюша
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад