Наклонная длиной 12 см образует с плоскостью угол 30°. Определите длину проекции этой наклонной на плоскость.
Ответы
Ответ дал:
0
Решение:
АВ = 12 (см.) - в нашем случае это гипотенуза.
Надо найти перпендикуляр,а после чего и проекцию.
Так как сторона,которая лежит против угла в 30 градусов,в два раза меньше гипотенузы,то перпендикуляр равен:
1) 12:2 = 6 (см.) - перпендикуляр.
Так как это прямоугольный треугольник,то за теоремой Пифагора найдем проекцию:
2) √12^2-√6^2=108=6√3(см.) - проекция.
Ответ:6√3
Ответ дал:
0
Ответ:
6
Пошаговое объяснение:
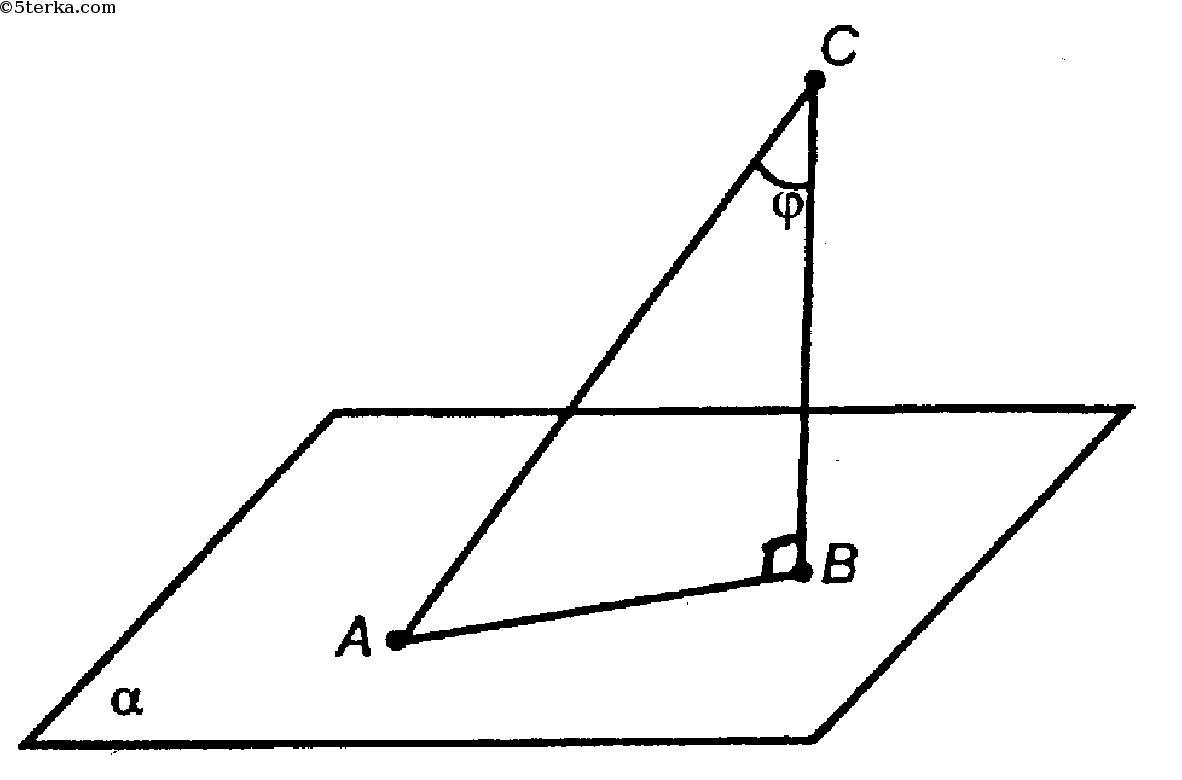
АС = 12 см - наклонная, СВ - перпендикуляр к плоскости , АВ - проекция АС на
ΔАВС (∠В=90°)
По теореми синусов
Сумма всех углов треугольника равна 180°, поэтому ∠С=180°-(∠А+∠В)=180°-(30°+90°)=60°
=
(sin90°=1, sin60°=
, АВ/
=
=
)
2AB=36
AB=
AB=
AB=6 (избавились от иррациональность)
АВ=6 - проекции
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад