Question

Объясните, как решать подобные задачи

Answer 1

Ответ:

(см. объяснение)

Объяснение:

• Начнем сначала с общей теории:

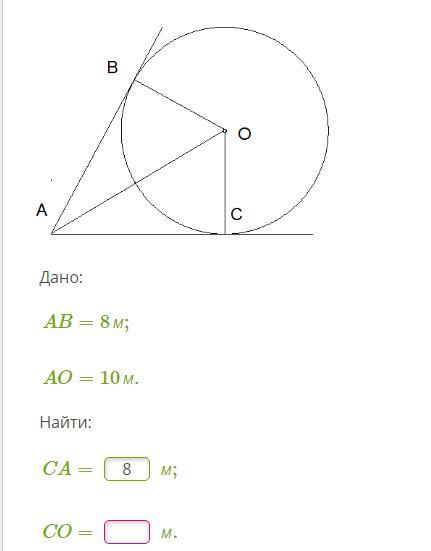
Радиус, проведенный к касательной в точку касания, перпендикулярен этой касательной, поэтому ∠ABO=∠ACO=90°. Покажем, что ΔABO=ΔACO. Действительно, оба этих треугольника имеют общую строну AO; также BO=CO=R - радиусы. Ссылаясь на прямоугольность и теорему Пифагора, получаем, что $AB=AC=\sqrt{AO^2-R^2}$. Значит по трем сторонам ΔABO=ΔACO (некоторые любят доказывать данное равенство, ссылаясь на малоизвестные признаки равенства прямоугольных треугольников, которые следуют из того, что написано мною выше). Из равенства треугольников следует, что ∠BAO=∠CAO, т.е. AO - биссектриса ∠BAC. Так мы показали, что:

1. AB=AC
2. AO - биссектриса ∠BAC

Это, пожалуй, вся необходимая теория. Добавлю еще только, что доказанные выше факты считаются очевидными и при решении не требуют доказательства (но понимать, откуда они берутся, естественно, надо).

• Теперь перейдем к решению:

Так как AB=CA, то CA=8. По теореме Пифагора для ΔACO $CO=\sqrt{100-64}=6$. Вот и все, что нужно записать.

Задача решена!