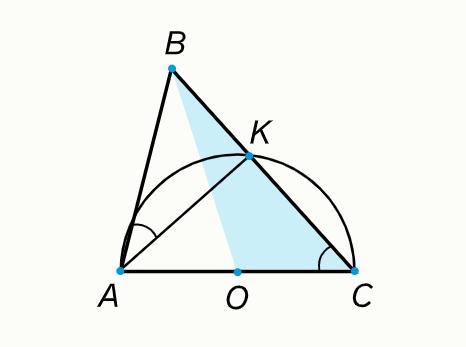
В треугольнике ABC известны стороны AC=14 и AB=6. Окружность с центром O, построенная на стороне AC как на диаметре, пересекает сторону BC в точке K. Оказалось, что ∠BAK=∠ACB. Найдите площадь треугольника BOC.
Приложения:
Ответы
Ответ дал:
9
Ответ:
Объяснение:
Если ∠BAK=∠ACB ,значит ВА - касательная к данной окружности и угол ВАК равен 90 градусов. Значит площадь треугольника АВС равна 14*6/2=14*3=42 кв.единицы. Учитывая,что АО=ОС ,а высота у треуголника АВС и ВОС одна и та же ВА получаем,что площадь треугольника образованного медианой и половиной основания равна половине данного АВС . Площадь ВОС равна 1/2 * АВС=1/2*42=21 кв. Ед.
Можно другим способом. ОС=1/2* СА=7 ед.
Высота перпендикулярна основанию и равна ВА = 6 ед.
Площадь равна 7*6/2=21 кв.ед.
GeniyVKybe:
Спасибо! Ответ проверенный.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
9 лет назад