Question

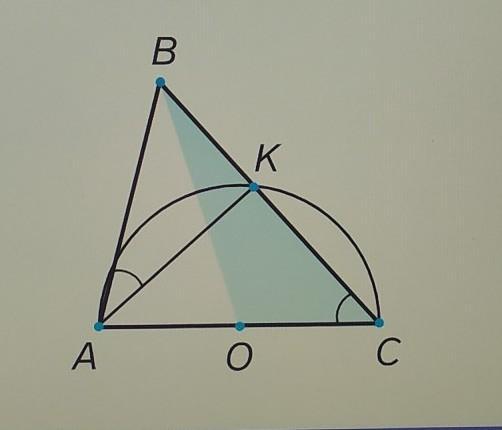
В треугольнике ABC известны стороны AC = 14 и АВ = 8. Окружность с
центром 0, построенная на стороне AC как на диаметре, пересекает сторону
ВС в точке К. Оказалось, что угол ВАК = уголACB. Найдите площадь
треугольника ВОС.​

Answer 1

Ответ:

28

Объяснение:

угол ACK = a, ak - высота (угол AKC прямой, так как AC - диаметр).

значит угол KAC = 90 - a, KAB = a, значит BAC = 90, тогда ABC - прямоугольный, значит AB и AC - катеты, тогда Sabc = 0,5*8*14 = 56. BO - медиана,  так как О - центр окружности, значит Sboc = 0,5*Sabc = 28