Question

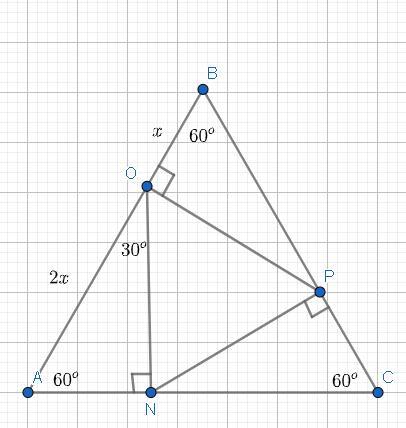
в равносторонний треугольник abc вписали другой равносторонний треугольник (см. рис.), стороны которого перпендикулярны сторонам треугольника ABC. В каком соотношении вершины вписанного треугольника делят стороны треугольника ABC?​

Answer 1

Так как ΔABC — равносторонний, то: $<A = \: <B = \: <C = 60^o.$

Это очень важно учитывать!

Стороны вписанного треугольника — перпеникулярны сторонам исходного треугольника ABC, то есть:

$ON \perp AC; \: NP \perp BC;\: NO \perp AB.$

То есть, образуются прямоугольные треугольники: $\triangle ANO; \: \triangle OBP; \: \triangle NPC.$

И так как углы исходного треугольника равны 60°, то:

$<A = 60^o \Rightarrow <AON == 90-60 = 30^o;\\<C = 60^o \Rightarrow <CNP = 90-60 = 30^o;\\<B = 60^o \Rightarrow <OPB = 90-60 = 30^o.$

Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.

То есть:

$AN = AO/2;\\PC = NC/2;\\OB = BP/2.$

Также, эти прямоугольные треугольники друг другу равны, по двум углам (60°; 30°), и по одному катету: OP ≡ NO ≡ NP, так как вписанный треугольник — равносторонний.

И так как: $AN \equiv OB \Longrightarrow \: OB = AO/2 \Rightarrow AO = 2x; \: OB = x.$

Вывод: Вершины вписанного треугольника делят сторону исходного треугольника в отношении: 2:1.