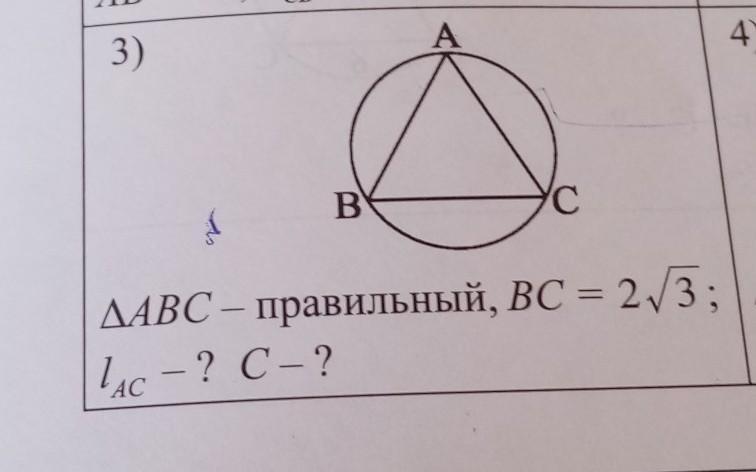Ответы
Ответ дал:
0
Чтобы найти длину дуги AC, для начала найдём радиус описанной окружности:
Радиус равен 2 ед.
Так как треугольник ABC — правильный, то каждый внутренний угол равен 60°.
Напротив вписанного угла B — лежит дуга AC, а теорема о вписанной угле окружности такова: вписанный угол равен половине градусной меры дуги, на которую он опирается.
То есть: ∪AC = <B*2 = 60*2 = 120°.
То есть: Центральный угол, противоположный дуге AC равен 120°.
Формула вычисления длины дуги, зная центральный угол, и радиус:
Длина окружности равна:
Вывод: 4.2 ед.; C = 12.57 ед.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад