Question

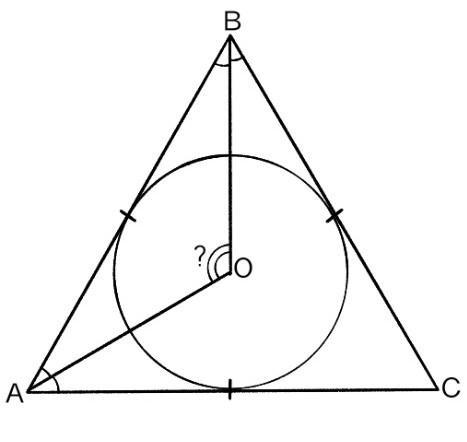
5. Коло з центром у точці О дотикається сторін рівносторон-
нього трикутника АВС. Знайдіть кут АОВ.

Answer 1

Дано:

∆АВС — равносторонний.

О — центр окружности.

Найти:

∡АОВ = ?

Решение:

Так как окружность касается сторон ∆, то это вписанная окружность в ∆ (по определению).

Соединим точки А и О ; В и О отрезками и рассмотрим получившиеся ∆АОВ.

АО — биссектриса ∡ВАС, ВО — биссектриса ∡АВС, так как О — центр вписанной в правильный ∆ окружности, а по совместительству это ещё и инцентр (точка пересечения биссектрис).

Тогда ∡ВАО = ∡АВО = 60° : 2 = 30°, так как углы правильного ∆ равны между собой и равны по 60°.

По теореме о сумме внутренних углов ∆ :

∡АОВ + ∡ВАО + ∡АВО = 180°

∡АОВ = 180° - ∡ВАО - ∡АВО = 180° - 30° - 30° = 120°.

Ответ : 120°.