Question

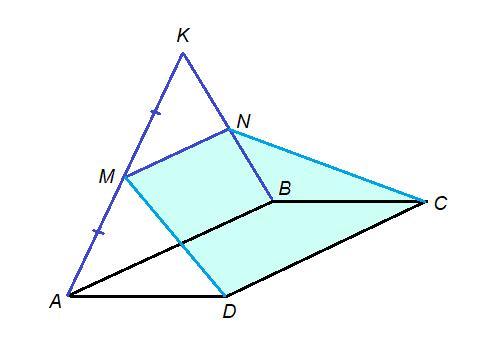
а). Трикутник КАВ і паралелограм ABCD мають спільну
сторону АВ і лежать у різних площинах. Через сторону
CD і точку M – середину відрізка АК - проведено пло-
щину, яка перетинає КВ у точці N.
а) Доведіть, що прямі MNi AB паралельні.
б) Знайдіть AB, якщо MN = 5 см.
в) Визначте вид чотирикутника MNCD.​

Answer 1

Ответ:

б) АВ = 10 см

в) MNCD - трапеция.

Объяснение:

а)

CD║AB как противолежащие стороны параллелограмма,

АВ ⊂ (КАВ), значит CD║(КАВ) по признаку параллельности прямой и плоскости.

• Если через прямую, параллельную некоторой плоскости, проходит плоскость, пересекающая данную плоскость, то линия пересечения плоскостей параллельна данной прямой.

CD параллельна плоскости треугольника КАВ, плоскость (MCD) проходит через CD и пересекает плоскость (КАВ) по прямой MN, значит MN║CD.

MN║CD, CD║AB, значит MN║AB.

б)

М - середина АК, MN║AB, значит по теореме Фалеса

N - середина КВ, то есть MN - средняя линия ΔКАВ.

• Средняя линия треугольника равна половине стороны, с которой она не имеет общих точек.

MN = 0,5 AB = 5 см

АВ = 2MN = 2 · 5 = 10 см

в)

MN║CD, но MN ≠ СD, значит MNCD - трапеция.