Ответы
Ответ дал:
2
Ответ:
Спасибо за ответ, но это не правильно))) я уже решил
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад
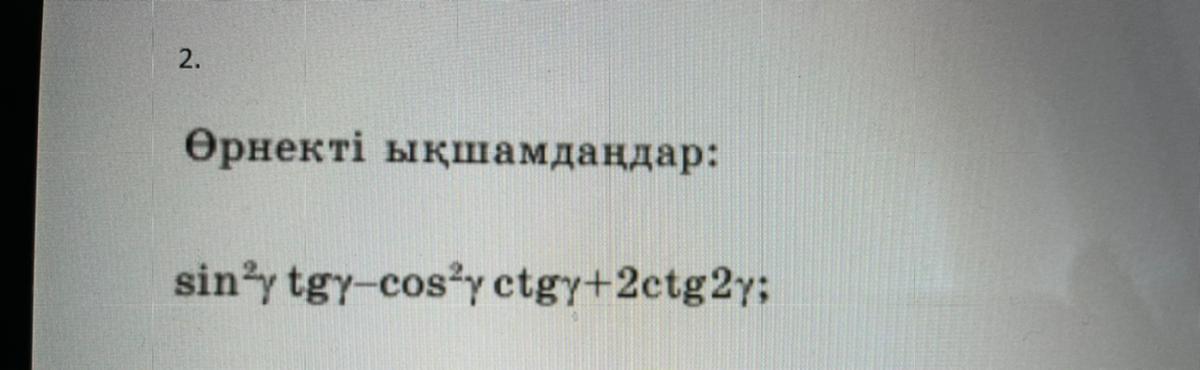
https://znanija.com/task/44820734?utm_source=android&utm_medium=share&utm_campaign=question