Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 3:2 считая от вершины угла при основании треугольника. Найди стороны треугольника, если его периметр равен 64 см.
Длины сторон запиши в порядке возрастания через точку с запятой.
ПОЖАЛУЙСТА ОЧЕНЬ НУЖЕН ОТВЕТ!!!!!
Ответы
Ответ дал:
1
Ответ:
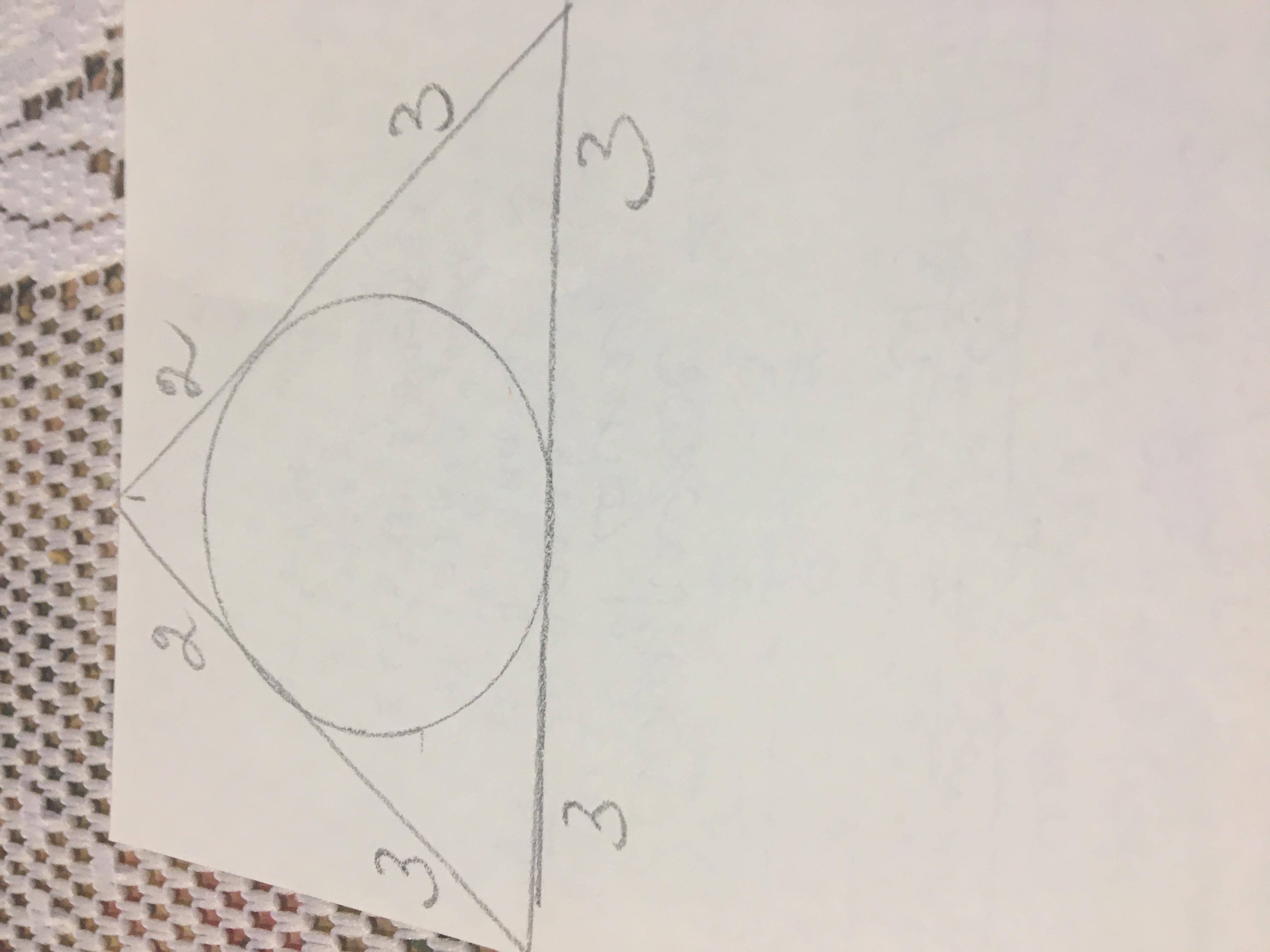
Тут используется теорема о касательных,которые проведены из 1 точки
2+2+3+3+3+3=16 частей
Одна часть равна
64:16=4 см
Основание равно 4•6=24 см
Каждая боковая сторона равна
4•5=20 см
Проверка
24+20+20=64 см
Объяснение:
Приложения:
trushinsemendom:
спасибо!!!!, ты просто спас
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад