Question

ABO=
BAO=
AOB=
Не влезло

Answer 1

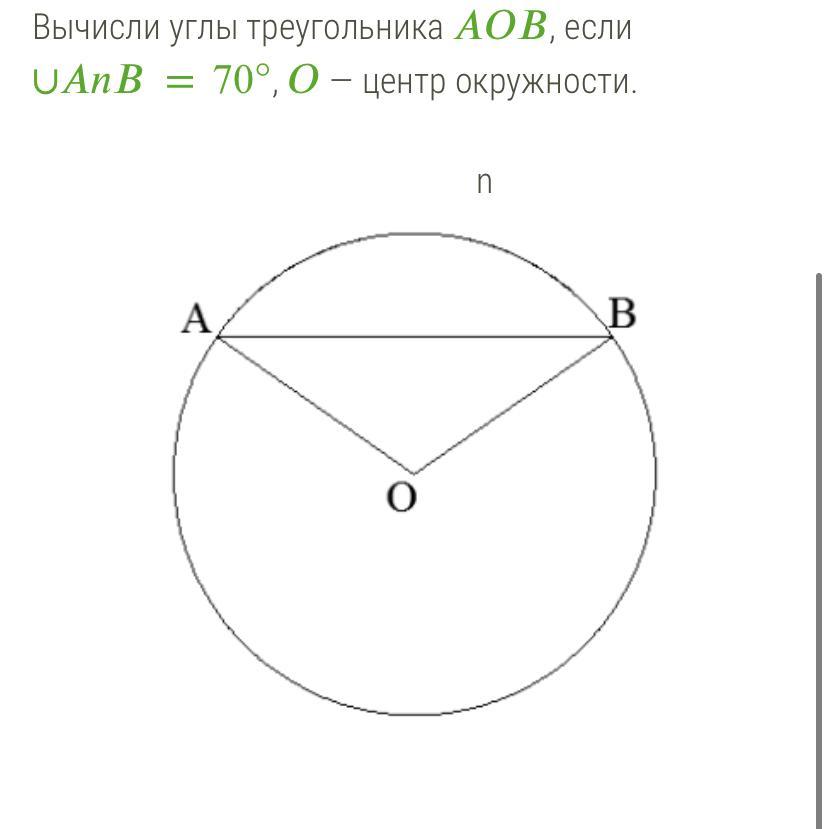
∠ABO - центральный, опирающийся на дугу AB - следовательно, он равен ей, и составляет 70°.

OA и OB - радиусы в окружности, соответственно, они равны, а значит, треугольник ABO - равнобедренный; следовательно, ∠OAB=∠OBA=(180°-70°)/2=55°.

Ответ: ∠AOB=70°, ∠OAB=∠OBA=55°.

Answer 2

Ответ:

70°,55°,55°

Объяснение:

Центральный угол равен дуге лежащей напротив этого угла. ⇒

∠АОВ = 70°

Т.к. АО и ОВ - радиусы, то они равны. ⇒

ΔАОВ - равнобедренный ⇒

∠ОАВ = ∠ ОВА = (180° - 70°) / 2 = 55°