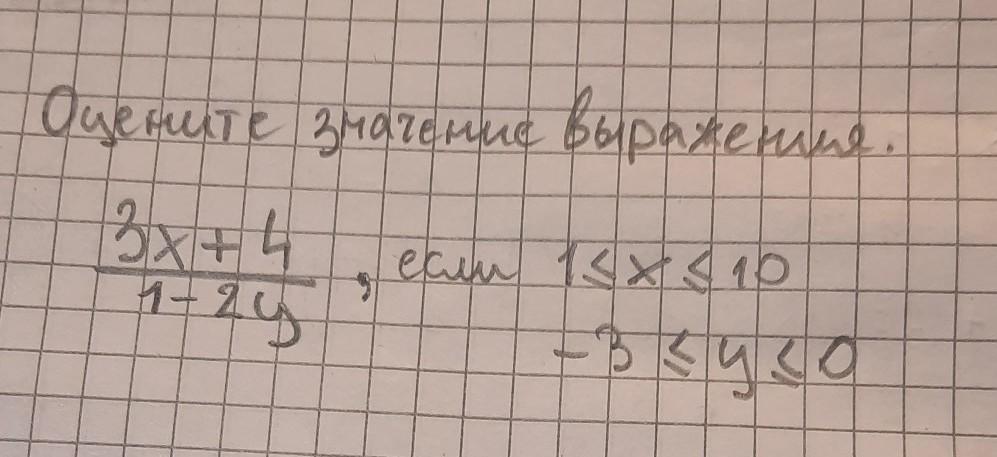Question

очень надо плиз ()()(​

Answer 1

Ответ:

$1 \leqslant \frac{3x + 4}{1 - 2y} \leqslant 34$

Пошаговое объяснение:

$\frac{3x + 4}{1 - 2y}; \: \: \: \: \: 1 \leqslant x \leqslant 10; \: \: \: - 3 \leqslant y \leqslant 0$

Определим ОДЗ для обеих переменных:

$ОДЗ :x \: \in \: \R; \: \: \: y \neq \frac{1}{2}$

1/2 - не входит в выбранный для у интервал.

Т.е. значение выражения определено и имеет смысл для любой пары х,у из выбранных интервалов.

Сделаем замену:

Пусть,

a= 3x + 4

b= 1 - 2y.

Оценим значения а и b:

$a = 3x + 4; \: \: 1 \leqslant x \leqslant 10 = > \\ = > 3 \times 1 + 4 \leqslant a \leqslant 3 \times 10 + 4 \\ 7 \leqslant a \leqslant 34$

Для оценки значения b меняем знаки неравенства на противоположные, т.к. у в нем представлен со знаком "-"

$b= 1-2y; \:\:\: - 3 \leqslant y \leqslant 0 = > \\ = > 1 -2 \times ( - 3) \geqslant b \geqslant 1 - 2 \times 0 \\ 1 \leqslant b \leqslant 7$

Итак, мы получили следующее:

$\begin{cases} \dfrac{3x + 4}{1 - 2y}; \\ 1 \leqslant x \leqslant 10; \\ - 3 \leqslant y \leqslant 0 \end{cases} < = > \begin{cases} \dfrac{a}{b}; \\ 7 \leqslant a \leqslant 34; \\ 1 \leqslant b \leqslant 7 \end{cases}$

При принятии одной из переменных за константу, выражение монотонно относительно второй переменой. Следовательно, макс. и мин. значения выражения - при значениях а и b с концов данных интервалов:

при а = 7 или а = 34

и при b = 1 или b = 7.

Вычислим:

$\begin{cases} a=7; b=1 \\ \dfrac{a}{b} = \dfrac{7}{1} = 7\end{cases} \: \: \begin{cases} a=7; b=7 \\ \dfrac{a}{b} = \dfrac{7}{7} = 1\end{cases} \\ \begin{cases} a=34; b=1 \\ \dfrac{a}{b} = \dfrac{34}{1} = 34\end{cases} \: \: \: \begin{cases} a=7; b=1 \\ \dfrac{a}{b} = \dfrac{34}{7} \end{cases}$

Как видно,

1 < 34/7 < 7 < 34

Следовательно:

min(a/b) = 1

max(a/b) = 34

А значит:

$1 \leqslant \frac{3x + 4}{1 - 2y} \leqslant 34$