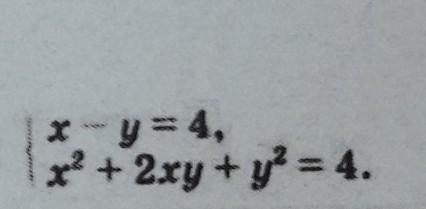Ответы
Ответ дал:
0
(3; - 1), (1; - 3)
Решение задания
Приложения:

Ответ дал:
2
Объяснение:
Ответ: (1;-3), (3;-1).
rudirayn568:
помоги пж 5. [2] Выполните действия: 3a + 4 - 16/(4 - 3a)
Решил. Смотри выше.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад