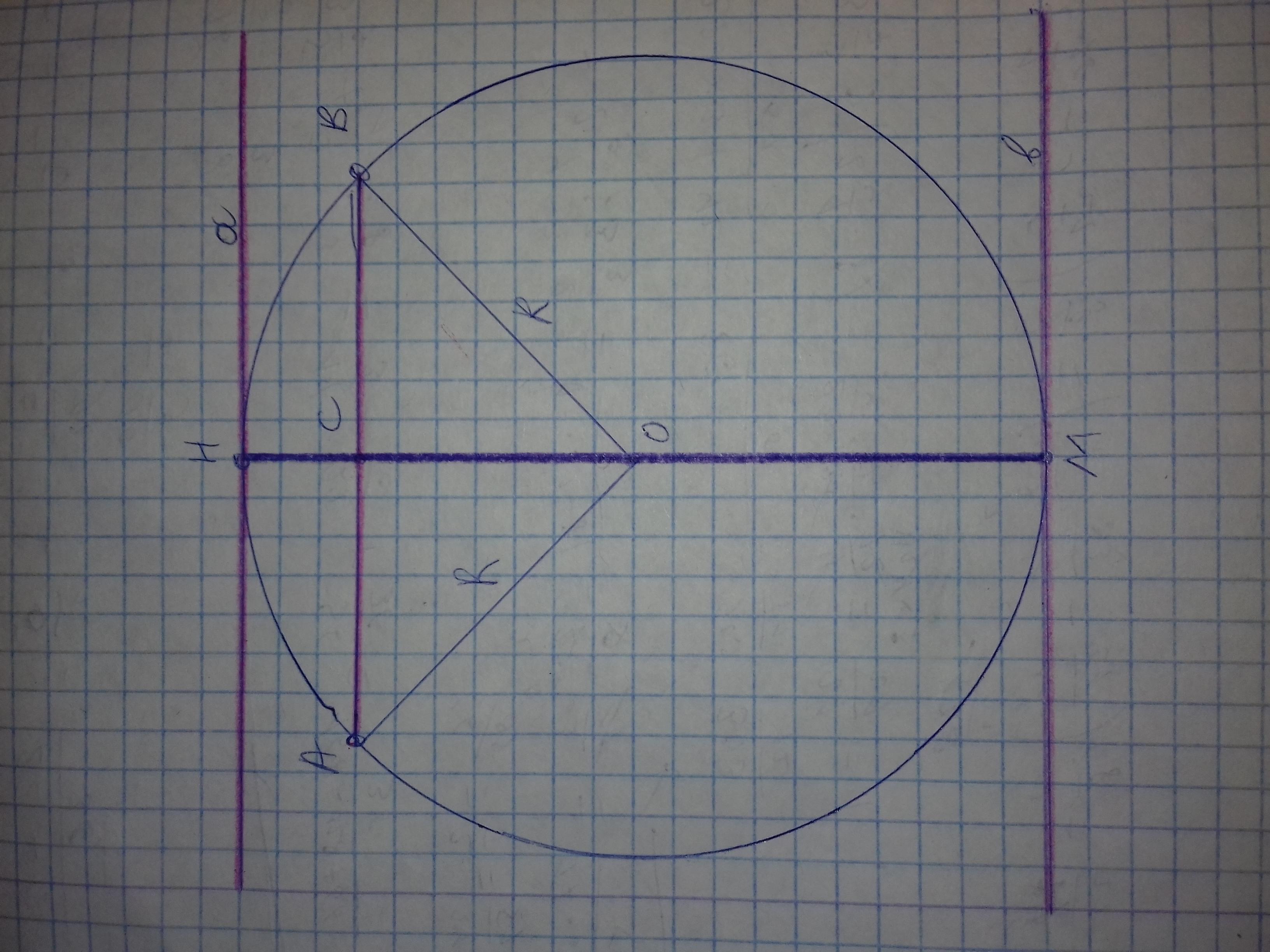
Докажите, что если через середину хорды провести диаметр, а через его концы-касательные к окружности, то хорда будет параллельна касательным.
Ответы
Объяснение:
..........................

Відповідь:
Прямые а, в и хорда АВ параллельны между собой.
Пояснення:
Пусть есть хорда АВ и точка С - ее середина. Проведем через центр окружности - точку О и центр хорды - точку С диаметр МН ( точки М и Н - лежат на окружности ). Проведем через точки М и Н две прямые а и в, касательные к окружности. Так как а и в касательные, построенные на диаметре МН, то а и в перпендикулярны к МН.
Докажем, что хорда АВ перпендикулярна МН. Рассмотрим треугольники АСО и ВСО. Они равны, так как АО = ВО = R, АС = ВС ( по условию задачи точка С - середина АВ ), сторона СО - общая. Треугольник АВО - равнобедренный с основанием АВ, СО - медиана, проведенная к АВ. В равнобедренном треугольнике медиана проведенная к основанию является высотой, а значит АВ перпендикулярна к СО и следовательно к МН.
Прямые а, в и хорда АВ перпендикулярны к диаметру МН, а следовательно прямые а, в и хорда АВ параллельны между собой.