Question

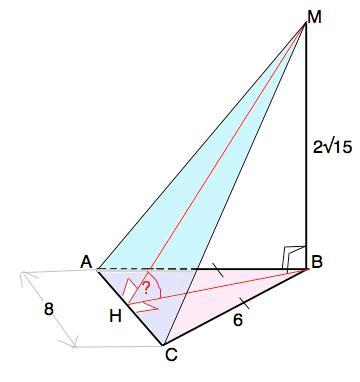
Через вершину В треугольника АС, в котором АВ = ВС = 6 см, АС = 8 см, проведены перпендикуляр МВ к плоины треугольника. Найдите угол между плоскостями АВС и АМС, если МВ = 2√15см. ПОЖАЛУЙСТА ГЛАВНОЕ РИСУНОК

Answer 1

Ответ: 60°

Объяснение:

    Угол между плоскостями –  двугранный угол.  Его величина  определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.

   Отрезок МВ по свойству перпендикуляра к плоскости перпендикулярен любой прямой в этой плоскости. ВН - высота ∆ АВС ⇒  ∆ МВН - прямоугольный.

  В плоскости АВС  отрезок ВН перпендикулярен АС ( ребру двугранного угла), в плоскости АМС - наклонная МН, АС по т. о 3-х перпендикулярах. Угол МНВ - искомый.

ВН - высота и  медиана ∆ АВС, поэтому АН=НС=4 (см).

По т.Пифагора ВН=√(ВС²-СН²)=√(36-16)=2√5 (см)

tg MHB=МВ:НВ=(2√15):2√5=√3

√3–тангенс 60°. Угол МНВ=60°