Question

Сторона правильной четырехугольной пирамиды равна 10см, а боковое ребро – 12см. Найдите площадь полной поверхности пирамиды.
Необходимо полное решение задачи ​

Answer 1

Ответ:

100+20√119 см²

Объяснение:

Дано:

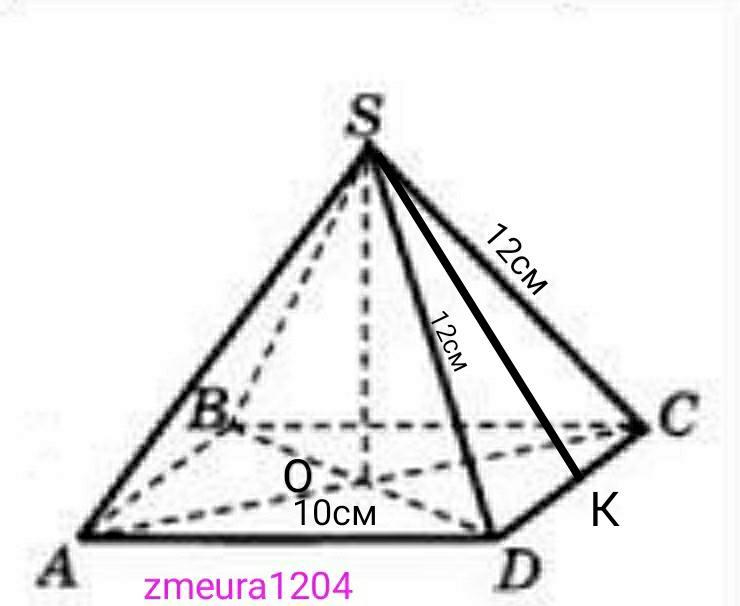
SABCD- пирамида

ABCD- квадрат

АВ=10см

SC=SD=12см.

Sпол=?

Решение

∆SCD- равнобедренный треугольник

SK- высота и медиана.

DK=KC=5см

По теореме Пифагора

SK=√(SD²-SC²)=√(12²-5²)=√(144-25)=

=√119см.

Росн=4*АВ=4*10=40см

Sбок=1/2*SK*Pосн=1/2*40*√119=20√119см²

Sосн=АВ²=10²=100см²

Sпол=Sбок+Sосн=100+20√119 см²