Question

даю 30 баллов решите пж
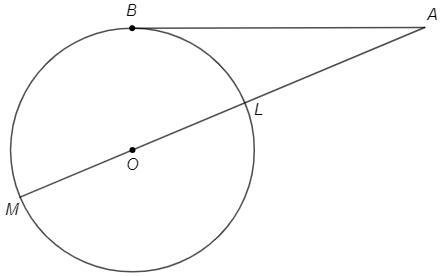
К окружности с центром в точке O проведены касательная AB и секущая AO (B - точка касания). Отрезок AO пересекает окружность в точке L. Известно, что AB = 12, AL = 8. Найдите радиус окружности.

Answer 1

Продлим AO: LM - диаметр (=2r), AM - секущая

Теорема о касательной и секущей:

Произведение секущей на ее внешнюю часть равно квадрату касательной

AB^2 =AM*AL

12^2 =(2r +8)*8 => 18 =2r +8 => r =(18-8)/2 =5