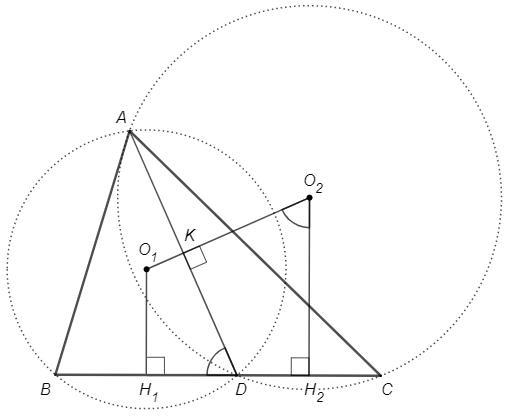
На стороне ВС треугольника ABC отмечена точка D.
Найдите сторону ВС, если расстояние между центрами окружностей, описанных около треугольников ABD и ACD, равно d и <ADB= a.
Ответы
Ответ дал:
4
Центр описанной окружности - пересечение серединных перпендикуляров.
O1O2, O1H1, O2H2 - серединные перпендикуляры к AD, BD, DC
H1D=BD/2, DH2=DC/2 => H1H2 =BC/2
KO2H2D - описанный четырехугольник (противоположные углы прямые).
Внешний угол описанного четырехугольника равен противолежащему внутреннему.
O2 =ADB =a
H1H2 - проекция O1O2 на BC.
H1H2 =O1O2 sin(O2) =d sina
BC =2H1H2 =2d sina
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад