Ответы
Ответ дал:
1
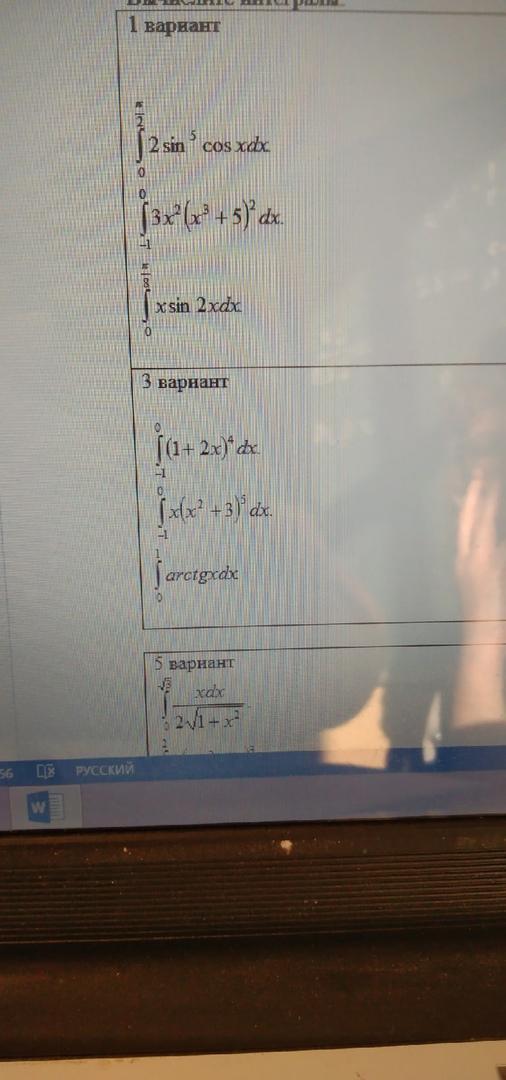
1 вариант
1.
2.
3.
3 вариант
1.
2.
3.
Чем вы пользовались при решение, если это какой то сайт можете пожалуйста дать ссылку
это мое решение, не сайт
Понятно, спасибо большое))
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад