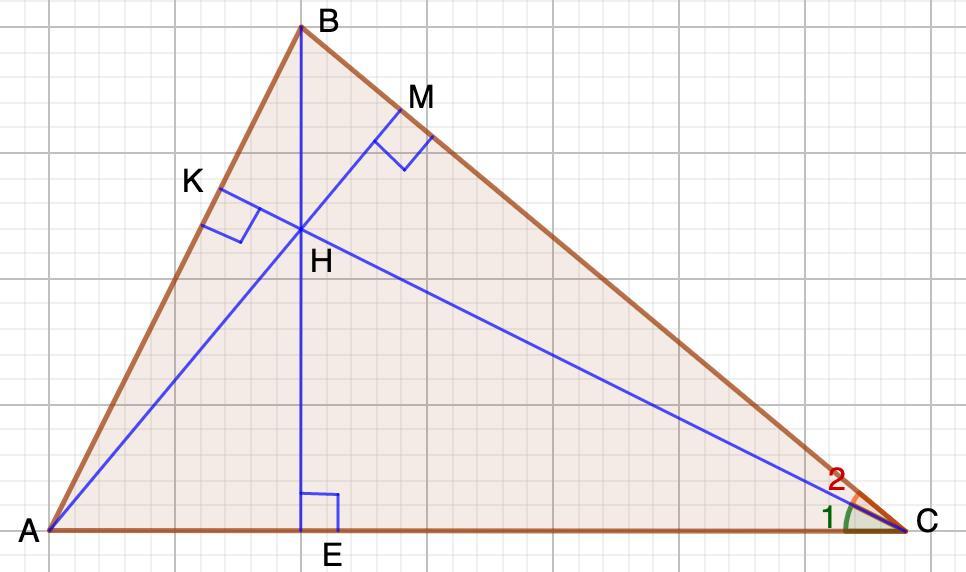
Точка H — ортоцентр остроугольного треугольника ABC. Известно, что AH⋅BC=9, BH⋅AC=30, а площадь треугольника ABC равна 18. Найдите CH⋅AB.
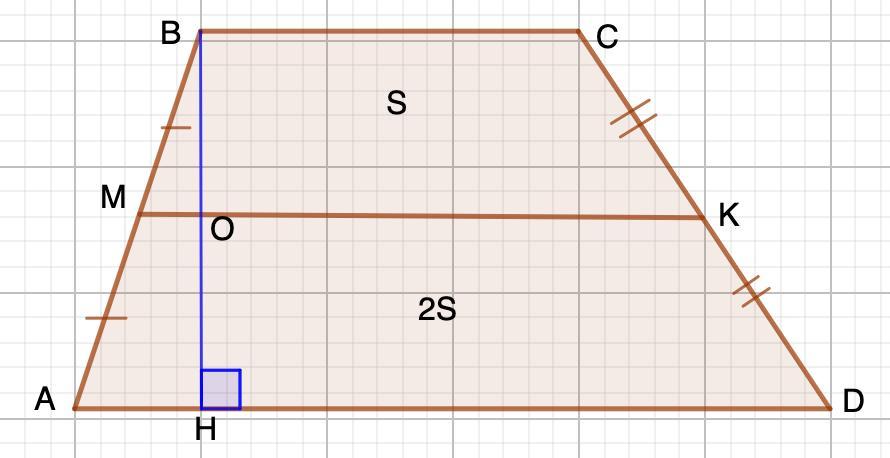
Средняя линия трапеции делит трапецию на две, площадь одной из которых в 2 раза больше площади другой. Найдите отношение большего основания исходной трапеции к меньшему.
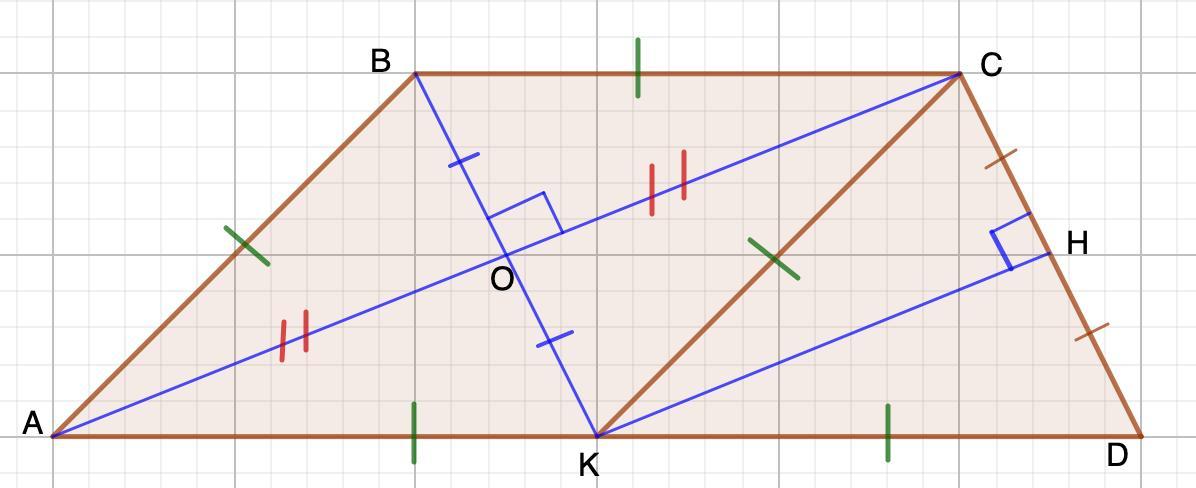
В трапеции ABCD с основаниями AD и BC выполнено равенство AD=2AB=2BC. Диагональ AC равна 7, а боковая сторона CD равна 5. Найдите площадь трапеции.
Решите срочно пжжжпжпжжжпжпж даю 81 балл!!!!
Ответы
Ответ:
1. CH * AB = 33
2.
3. квадратных сантиметров
Объяснение:
1. Дано: H — ортоцентр остроугольного ΔABC, ,AH⋅BC=9, BH⋅AC=30.
Найти: CH⋅AB - ?
Решение: По определению ортоцентр(точка H по условию) эта точка пересечения высот треугольника, при этом по свойствам ортоцентра в остроугольном треугольнике (по условию ΔABC - остроугольный) ортоцентр лежит внутри треугольника.
Составим системы уравнений по формуле площади треугольника и условию задачи:
1) 2)
1) 2)
Поделим нижнее уравнение системы на верхнее уравнение:
1)
2)
Составим систему уравнений:
Составим систему уравнений:
Продолжение решения задач (задачи 2,3) смотрите в вордовском файле!!!
Ответ:
Объяснение:
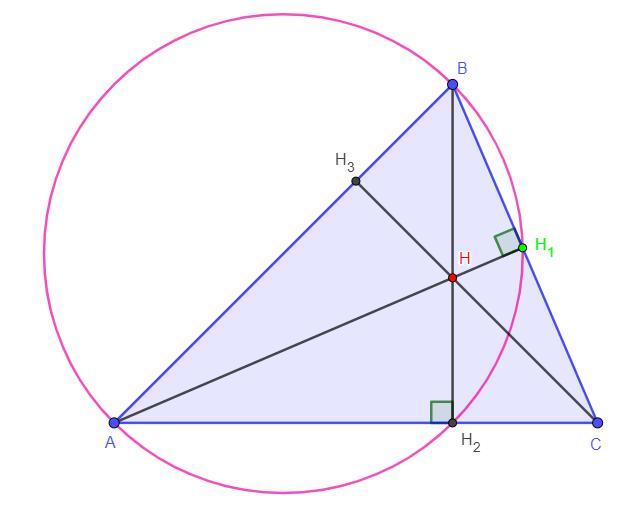
I. Дано: ΔАВС - остроугольный.
Точка Н - ортоцентр, то есть точка пересечения высот.
АН·ВС=9; ВН·АС=30;
Найти: СН·АВ
Решение:
1.
2.
3. Рассмотрим ΔЕНС и ΔАКС - прямоугольные.
∠1 - общий
⇒ ΔЕНС ~ ΔАКС
4. Рассмотрим ΔНМС и ΔКВС - прямоугольные
∠2 - общий
⇒ ΔНМС ~ ΔКВС
5. Найдем АВ
6. Найдем искомое произведение:
II. Дано: ABCD - трапеция
МК - средняя линия
Найти: AD:BC
Решение:
Пусть ВС=х; AD=y
⇒
(МК - средняя линия)
Уравняем площади верхней и нижней трапеций согласно условию:
III. Дано: ABCD - трапеция
AD=2AB=2BC
AC=7; CD=5
Найти:
Решение:
Отметим точку К - середину AD
1. Рассмотрим АВСК
АВ=ВС (условие)
ВС=АК; ВС║АК (условие)
⇒АВСК - ромб
⇒АС⊥ВК; АО=ОС=3,5 (свойства ромба)
2. Рассмотрим ΔКCD
КС=КD (условие, построение)
⇒ ΔКCD - равнобедренный.
Проведем высоту КН ⇒КН - высота, медиана
⇒CH=HD
3. Рассмотрим ΔACD
CH=HD (п.2); AK=KD (построение)
⇒КН - средняя линия
⇒КН=7:2=3,5; КН║ОС
4. Рассмотрим КОСН
КН=ОС; КН║ОС; КН⊥CD; КВ⊥АС⇒КОСН-прямоугольник
⇒ОК=СН=2,5
5.