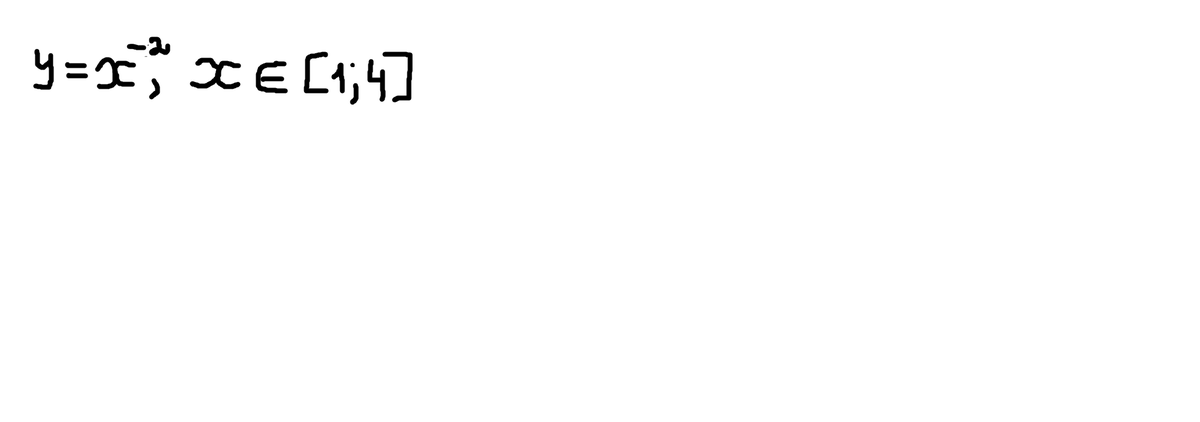Ответы
Ответ дал:
0
y = x^(-2) = 1/(x^2)
y' = -2/x^3 ≠ 0
На интервале x < 0 - функция возрастает
на интервале x > 0 - функция убывает, значит y(1) > y(4)
y(1) = 1/1 = 1 - наибольшее значение ф-ции на отрезке
y(4) = 1/4^2 = 1/16 - наименьшее значение ф-ции на отрезке
y' = -2/x^3 ≠ 0
На интервале x < 0 - функция возрастает
на интервале x > 0 - функция убывает, значит y(1) > y(4)
y(1) = 1/1 = 1 - наибольшее значение ф-ции на отрезке
y(4) = 1/4^2 = 1/16 - наименьшее значение ф-ции на отрезке
Ответ дал:
0
Ответ дал:
0
данная функция не монотонная. Она НЕ определена в точке х=0. Поэтому рассуждение все-таки не верное, хотя ответ верный.
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад
11 лет назад