Question

Диаметр окружности равен 9 см. Около неё описана равнобедренная трапеция, боковая сторона которой 15 см.
Вычисли основания и площадь трапеции.

1. Меньшее основание трапеции равно __ см,
2. большее основание равно __ см,
3. площадь трапеции равна __ см2.

Answer 1

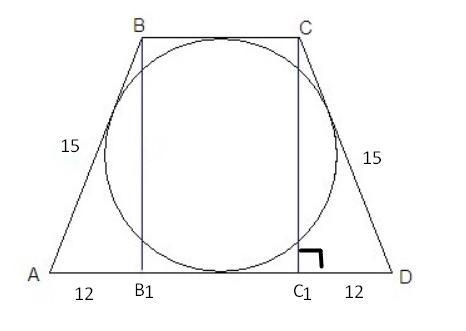
АВ=СD=15

ВС=? AD=? Sabcd = ?

Решение:

1) АВ=CD=BC+AD=15+15=30

2) Sabcd=(BC+AD)/2 * h = 30/2 * 9 = 15*9=135(см²)

3) BB₁ ⊥AD ; СС₁ ⊥ AD ⇒ АВ₁ = ВС₁ = ( AD-BC)/2

4) Р/м ΔСС₁D, ∠С₁=90°

   С₁D = $\displaystyle \sqrt{15^2-9^2} =\sqrt{225-81} =\sqrt{144} =12$

5) Пусть ВС=х, AD = 12+х+12=24+х

6) Средняя линия MN = (AD+BC)/2, а по условию (AB+CD)/2 т.е

    (24+х+х)/2 = 30/2  (*2)

            24+2х=30

                   2х=6

                    х=3 т.е ВС = 3(см)

АD=24+х=24+3=27(см)

Ответ: Sabcd = 135; AD = 27; BC=3