Question

13 БАЛЛОВ !!!
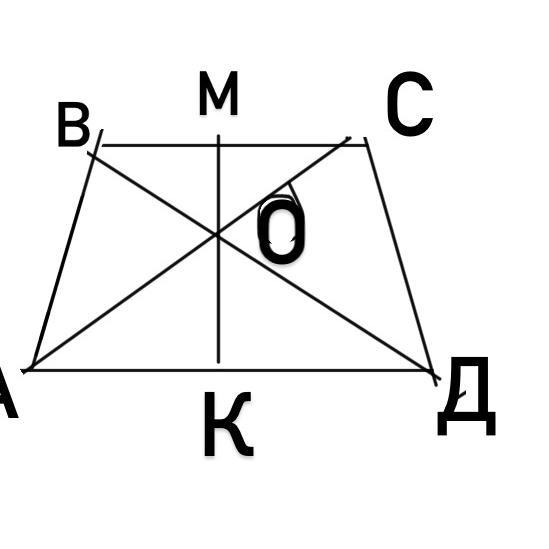
Точка О. Пересечение диагоналей трапеции АВСД. MK-произвольная прямая, проходящая через точку О. И пересекает основания.
Доказать что BМ относится к МС= DK относится к

Answer 1

Объяснение:

Дано:

Трапеция АВСD

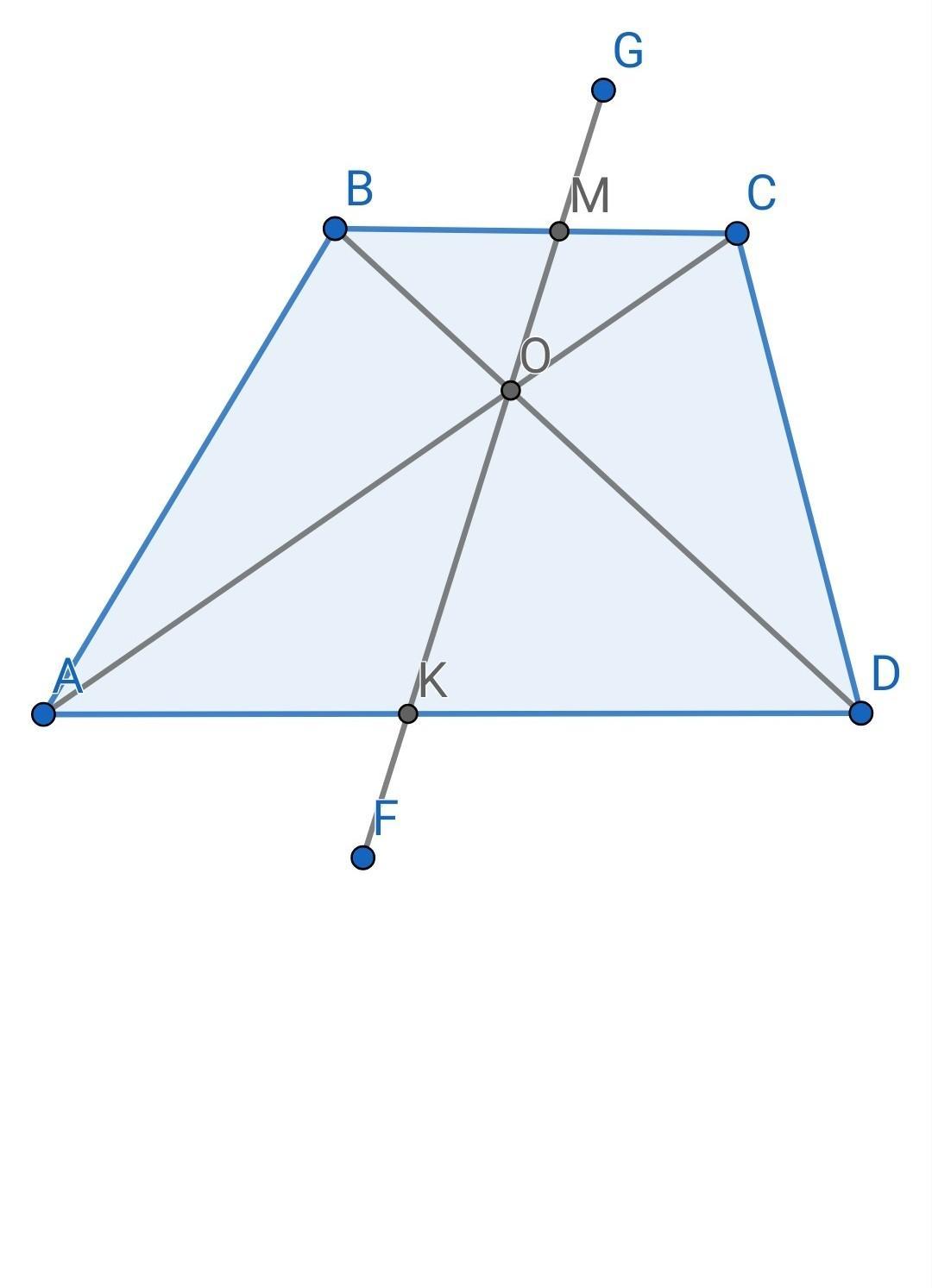
прямая FG

$AC \cap BD = O; \: \: O \in FG\\ FG \cap AD = K; \: FG \cap BC = M$

Доказать что

$\frac{BM}{MC}=\frac{DK}{AK}$

Доказательство

АВСD - трапеция => ВС || АD

Тогда диагонали АС, ВD и прямую FG можно рассматривать как секущие при 2х параллельных.

Соответственно,

- будут равны углы (как накрест лежащие):

$\angle CAD = \angle ACB; \: \: \angle ADB = \angle CBD; \\\ \angle DKM = \angle BMK; \: \: \angle AKM = \angle CMK$

- будут равны как вертикальные:

$\angle AOK = \angle COM; \: \angle KOD = \angle MOB$

Рассм. подобные ∆-ки.

Вследствие равенства углов подобны:

∆АОК и ∆СОМ

∆DОК и ∆BОМ.

Коэффициент подобия:

$\small{\triangle AOK \sim \: \triangle COM \: = > \frac{AK}{CM} ={\frac{OK}{OM}} = k_{1} ; \:} \\ \small{\triangle KOD \sim\triangle MOB = > \frac{KD}{MB} ={\frac{OK}{OM}} = k_{2}}$

Oчевидно, что в обоих случаях коэффициент подобия можно выразить через одно и то же соотношение, а значит коэффициенты равны:

$\small{{\frac{OK}{OM}} = \frac{OK}{OM} \: \: = > k_{1} = k_{2} \: = > \:} \\ = > \: \small{\frac{AK}{CM} {=}{\frac{DK}{BM}} < = >{AK}} {=}{\frac{DK \cdot CM}{BM}} { < }{ =}{ > }\\\small{ { < }{ =}{ > } \: \frac{AK}{DK} ={\frac{CM}{BM}}}$

Что и требовалось доказать