Объясните, почему производная функции  находится так
находится так  ? Почему не записываем производную
? Почему не записываем производную  , как
, как  ?
?
Приложения:
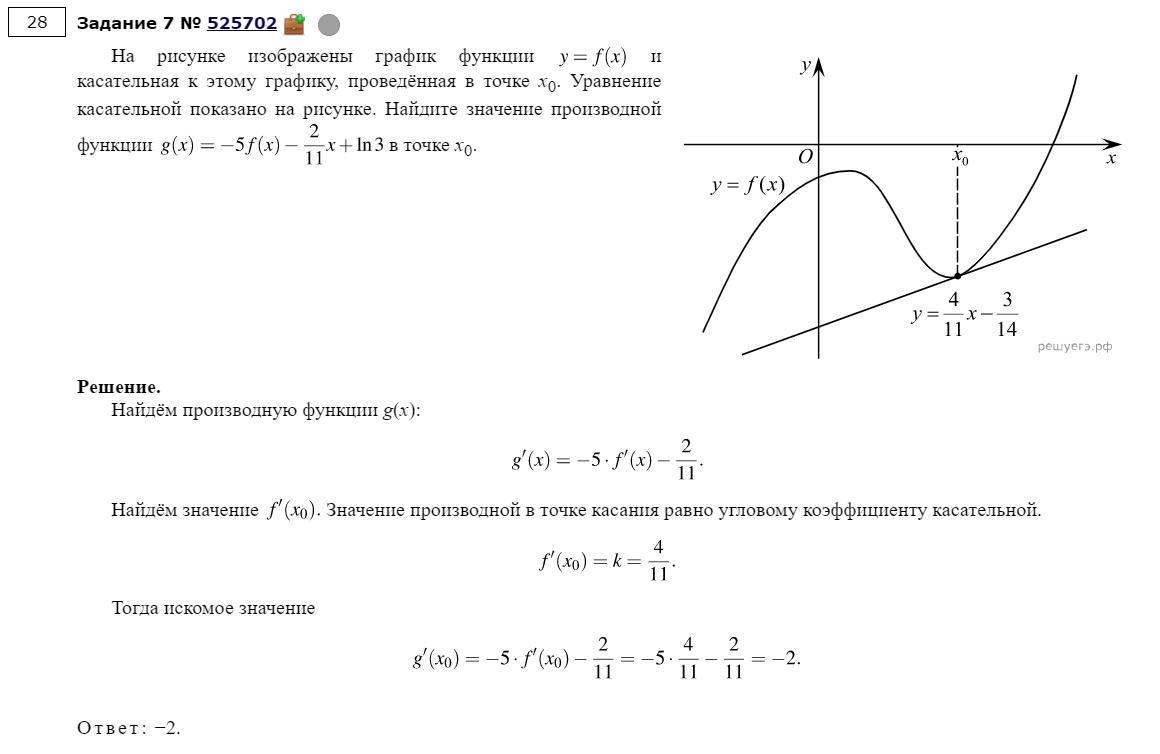
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
g'(x)= (-5·f(x))'-(2x/11)'+(ln3)'= -5·f'(x) - 2/11+0=-5·f'(x) - 2/11, т.к. ln3-сonst (постоянная), а производная постоянной величины равна 0.
NukoLeO:
Каким образом In3 стало константой? В таблице же производных равняется не нулю, а 1/x
ln3 -это постоянная величина, а вот lnx-переменная; (lnx)'=1/x, а (ln3)'=0
Вас заинтересует
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад