Ответы
Ответ дал:
1
Дано:
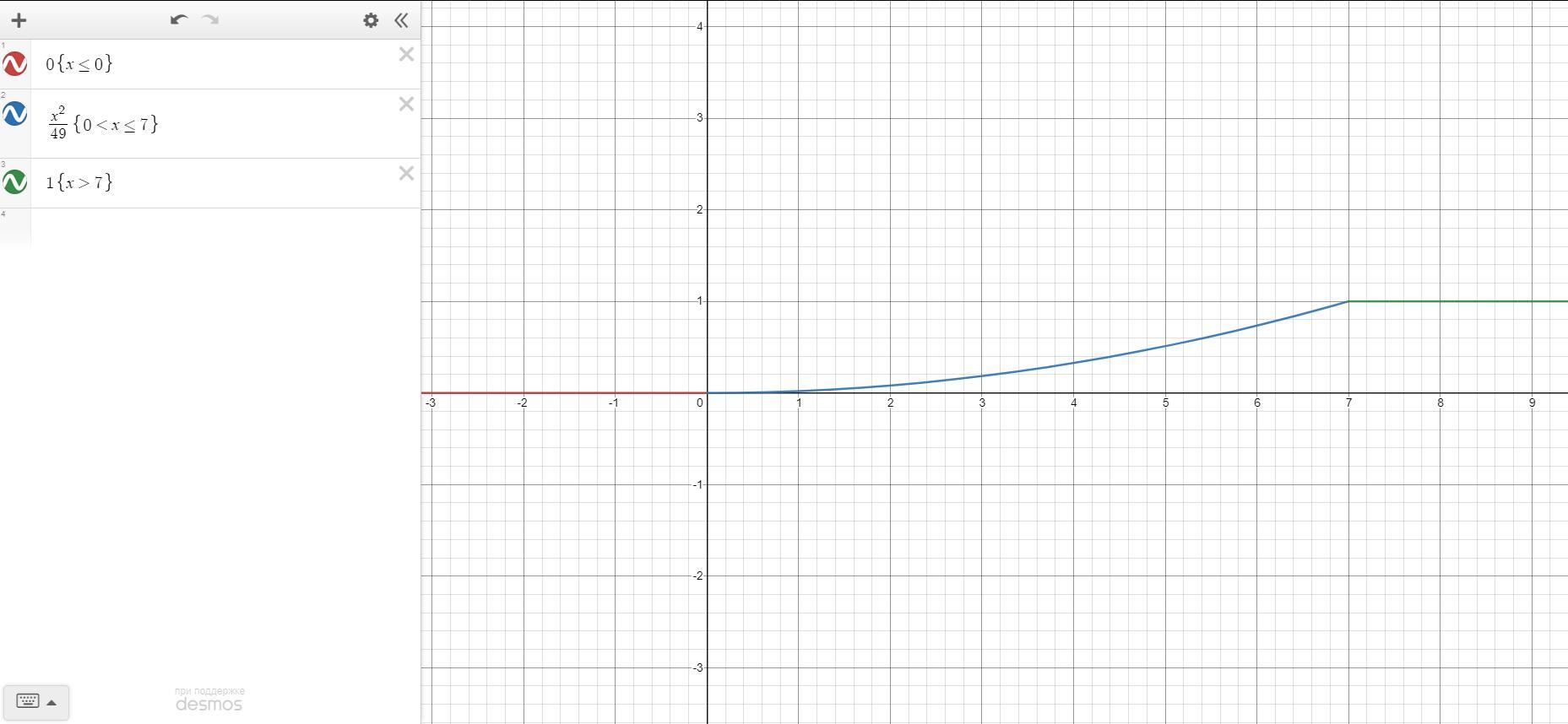
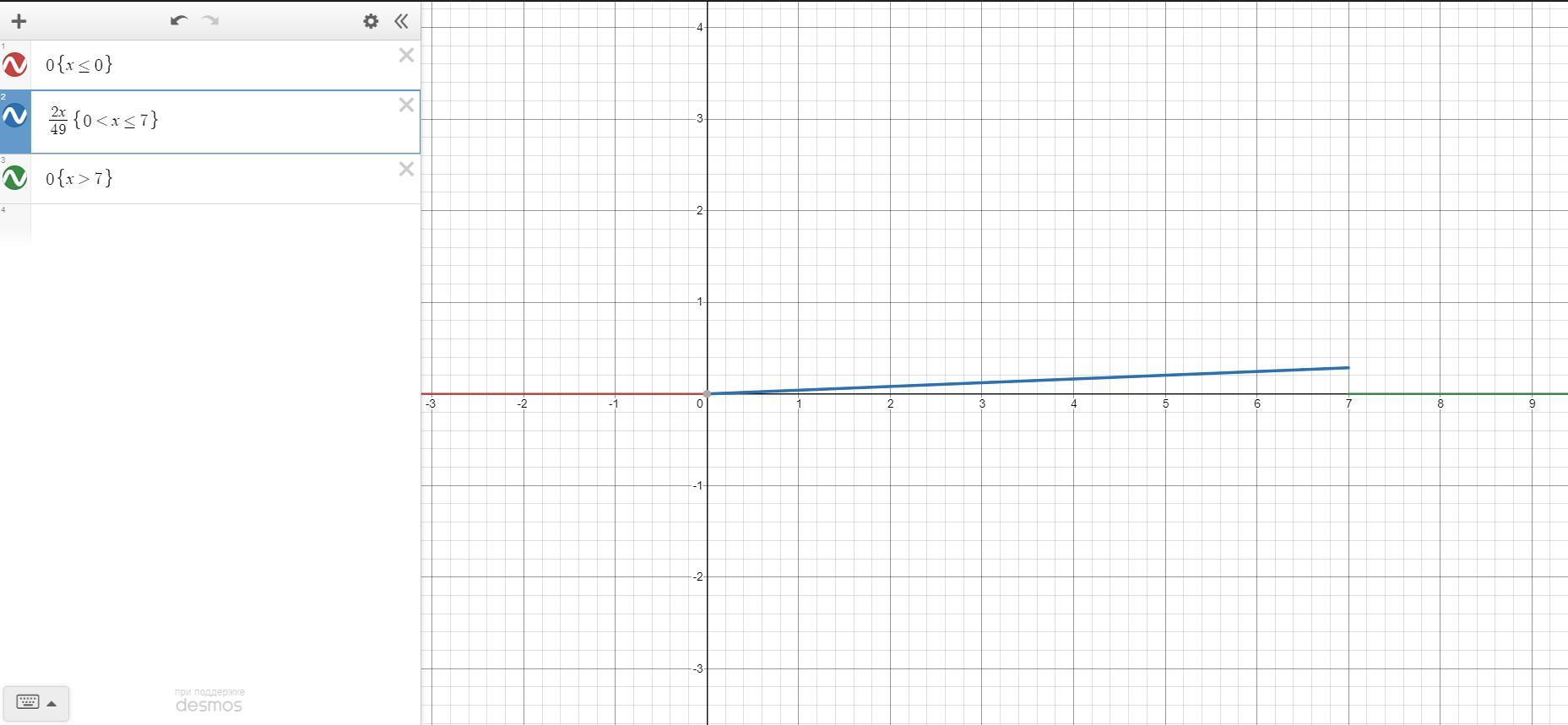
а) Плотность вероятности
б) Математическое ожидание
Дисперсия
в) Графики
График интегральной функции распределения плавный
График дифференциальной функции распределения имеет точку разрыва
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
