Question

Висота конуса дорівнює 2 см, а радіус основи —
4 см. Знайдіть площу перерізу, який проходить
через вершину конуса і хорду основи, що стягує
дугу 60°.

Answer 1

Відповідь:

8

Покрокове пояснення:

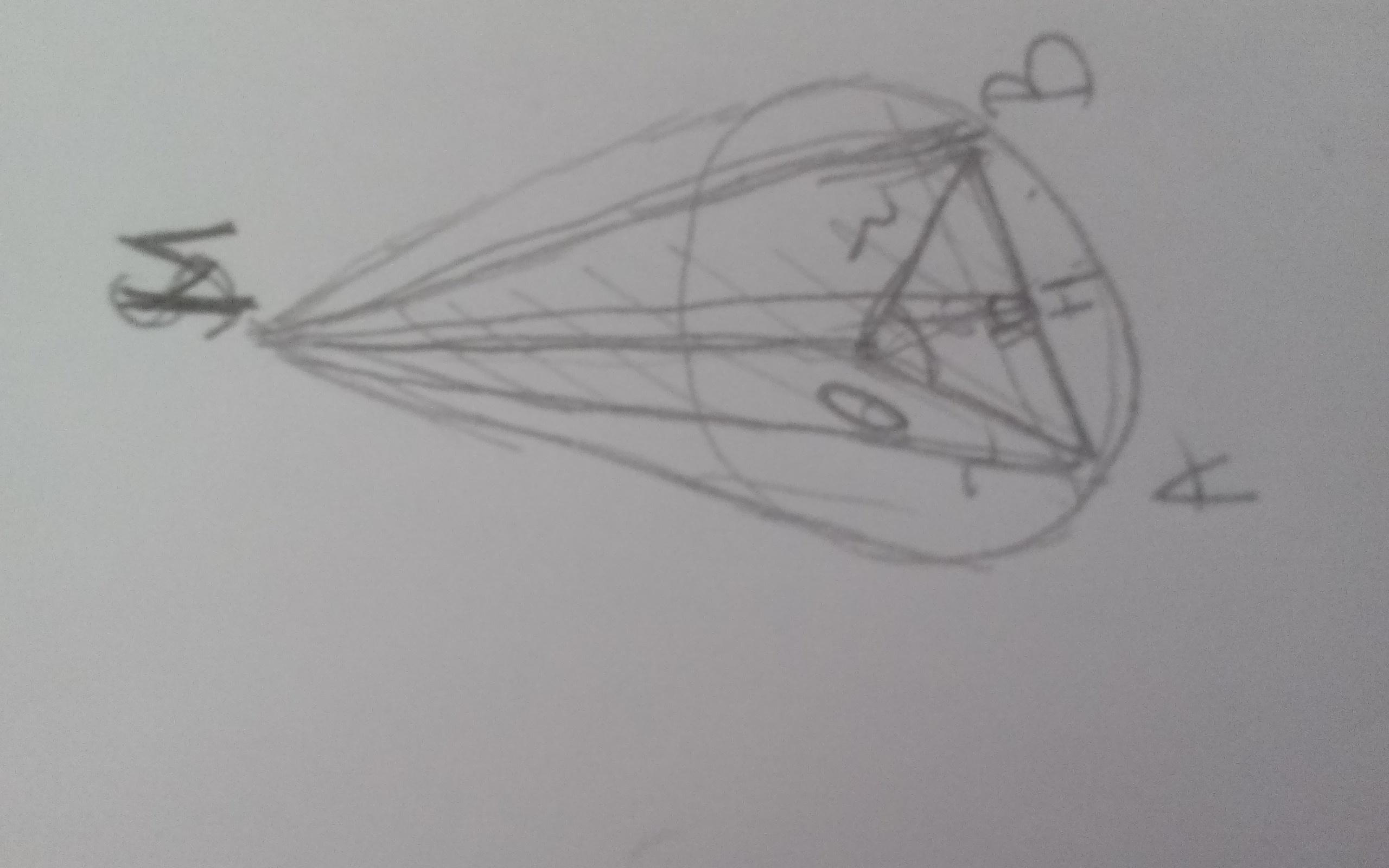
Нехай хорда АВ стягує дугу 60°.→/_ВОА=60° та ОВ=ОА, як радіуси → △ВОА рівносторонній та АВ=4см

Нехай М вершина конуса. Необхідно знайти площу △АМВ, який є рівнобедренним і МН-висота та медіана.

Розглянемо △ОМН, він прямокутний, |МО|=2 за умовою, а |ОН|=4√3/2=2√3, як висота △АОВ

За теоремою Піфагора |МН|=√(4+4×3)=4

S=1/2×4×4=8