молю! только, пожалуйста, понятным, русским языком объясните как это решать.. и желательно письменно на бумажке, потому что в символах тут фиг разберёшься... прошу я умираю
Приложения:
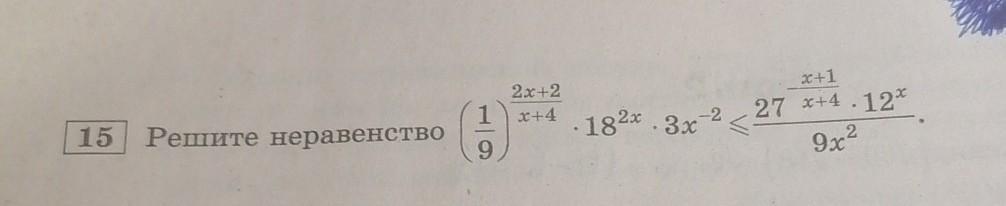
Ответы
Ответ дал:
1
Ответ:
Приложения:

dodjdjdo:
бог!
Вас заинтересует
2 года назад
3 года назад
10 лет назад
10 лет назад