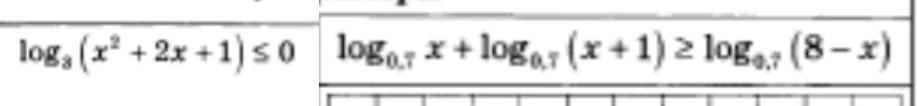Ответы
Ответ дал:
1
Відповідь:
Покрокове пояснення:
log_3 1=0 так как основа логарифма 3>1 можем записать x^2+2x+1<1 и ОДЗ: x^2+2x+1>0 → x≠-1
x^2+2x<0
x(x+2)<0 методом интервалов и учитивая ОДЗ
___+___-2___-___0____+____
Ответ:
хє(-2;-1)U(-1;0)
log_0.7 x+log_0.7(x+1)>=log_0.7(8-x)
log_0.7 x(x+1)>=log_0.7 (8-x)
Так как 0,7<1 меняем знаки уравнения
x(x+1)=<8-x и
ОДЗ: x(x+1)>0 &8-x>0 → хє(0;+inf)U(-1;+inf) & xє(-inf; 8)
______///////////////////////////////
_____-1______0////////////8////////
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Имеем ОДЗ хє(0;8)
x^2+x-8+x=<0
x^2+2x-8=<0.
x=-1±3
x1=2; x2=-4
(x-2)(x+4)=<0
__+___-4___-___2___+__
хє[-4;2]
Учитивая ОДЗ хє(-inf; -1)U(0;8)
_______-4//////-1///0//////2_____8___
_______________\\\\\\\\\\\\\\\\\\\
Ответ:
хє(0;2]
olgaua64:
Разобрались?
нет...откуда взялось -1 в примере
По лагорифмом функция должна бить >0
во втором x= -1+-3 что это? непонятно что вообще написали
а ответ како1
В первом номере хє(-2;-1)U(-1;0), во втором. хє[-3; -1)U(0;3]
x= -1 +-3 что это
Корни квадратного рехчлена, дискриминант равен 3
x1=-1; x2=3?
х1=-4 х2=2
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад