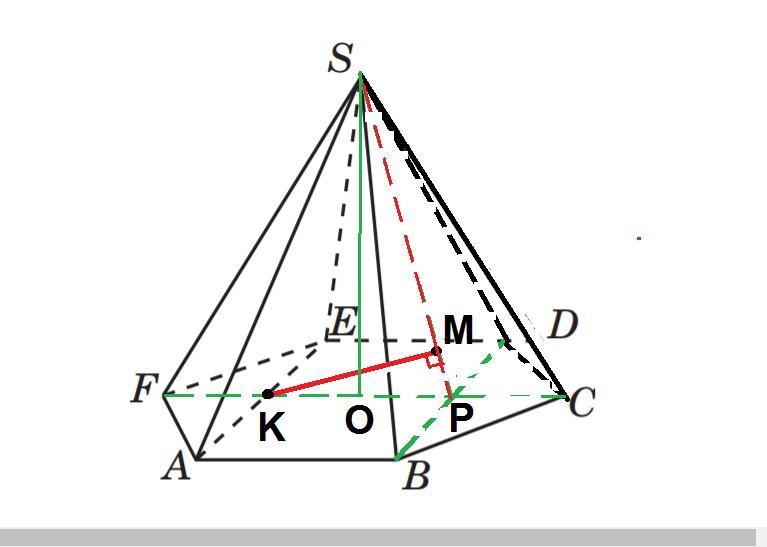
В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние между прямыми SB и AE.
стр 41 в документе
Ответы
Эту задачу можнорешить двумя способами.
1) Более лёгкий - геометрический.
Используется свойство: расстояние между прямыми L1 и L2 равно расстоянию от любой точки прямой L1 до плоскости P, параллельной прямой L1 и в которой находится прямая L2.
Проведём плоскость SBD, параллельную отрезку АЕ. След её сечения основания- это прямая BD.
Проведём секущую перпендикулярную плоскость FSC.
Точки К и Р это середины проекций боковых рёбер на основание.
В сечении имеем 2 равнобедренных треугольника FSC и KSP.
Высота их равна высоте пирамиды и равна √3 как высота равностороннего треугольника FSC со стороной 2.
Длина перпендикуляра КМ и есть искомое расстояние L1_L2.
Площадь KSP = (1/2)*1*√3 = √3/2.
Тогда КМ = 2S/(PS). Находим PS = √((√3)² + (1/2)²) = √13/2.
Ответ: КМ = 2*(√3/2)/(√13/2) = 2√3/√13 = 2√39/13.
2) Векторный способ или координатный.
Пусть вершина А на оси Ох в точке х = (√3/2), сторона ВС по оси Оу.
Наименование вершин по часовой стрелке.
Решение дано во вложениях как копии расчёта в программе Excel.
Ответ дан числом в десятичной системе, но его значение соответсвует найденному в варианте 1).