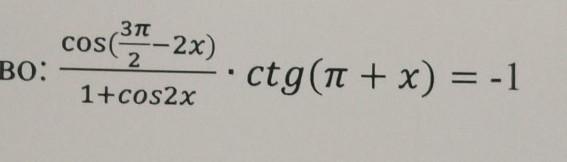Ответы
Ответ дал:
1
• Упростим числитель дроби:
cos(3π/2 - 2x) = - sin(2x)
• Упростим ctg(π + x):
ctg(π + x) = ctg(x) = cos(x)/sin(x)
• Перепишем в упрощённом виде:
- sin(2x)/(1 + cos(2x)) • cos(x)/sin(x) = - 1
(-2sin(x)cos(x) • cos(x))/((sin²(x) + cos²(x) + cos²(x) - sin²(x)) • sin(x) = -1
(-2sin(x)cos²(x))/(2cos²(x)sin(x)) = -1
-1 = -1
Тождество досказано ЧТД.
P.S. Формулы, которые я использовал:
sin²(x) + cos²(x) = 1
sin(2x) = 2sin(x)cos(x)
cos(2x) = cos²(x) - sin²(x)
ctg(x) = cos(x)/sin(x)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад