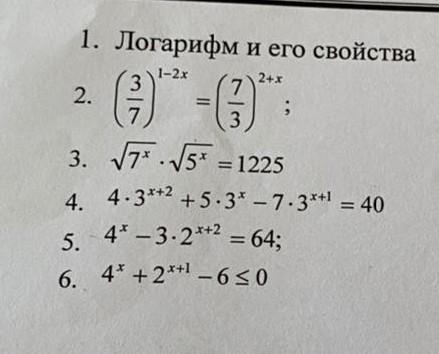Ответы
Ответ дал:
1
Ответ:
На первое оооочень долго отвечать, свойств много, как-нибудь сам скатай
Объяснение:
Приложения:

Ответ дал:
0
Ответ:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
10 лет назад