Question

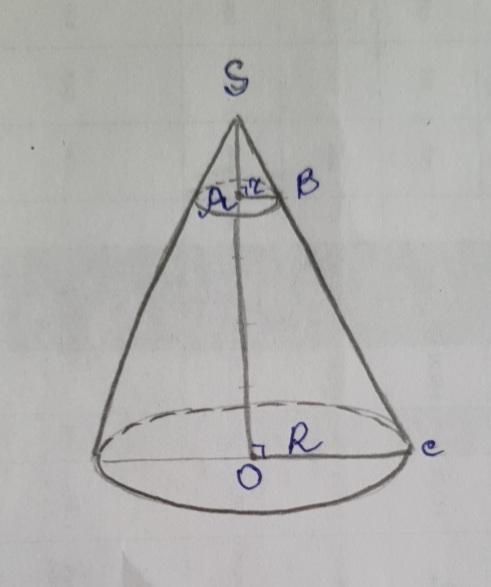
Через точку А высоты SO конуса проведена плоскость, параллельна основанию. Найдите площадь сечения, если площадь основания конуса равна 36корень2 см^2 и SA : AO = 1:5
Желательно с рисунком.

Answer 1

Ответ:√2.

Объяснение:

Площадь основания конуса равна 36√2.

Площадь основания конуса вычисляется по формуле S = π * R²

π * R² = 36√2 ⇒ R² = 36√2 / π

Рассмотрим ΔSAB и ΔSOC. Т.к. плоскость, проведенная через точку А параллельна основанию, то SA⊥АВ, SO⊥ОС - т.к. SO - высота.

SA:АО = 1:5 . Т.к. катеты одного прямоугольного треугольника пропорциональны катетам другого, то ΔSAB и ΔSOC - подобны.

Из подобия треугольников следует подобие сторон:

АВ:ОС = 1:6 - коэффициент пропорциональности k

r : R = 1 : 6 ⇒ r = R/6

Площадь сечения: S = π * r² = π *( R/6 )² =

= 36√2 / 36 = √2