Даю 100 баллов
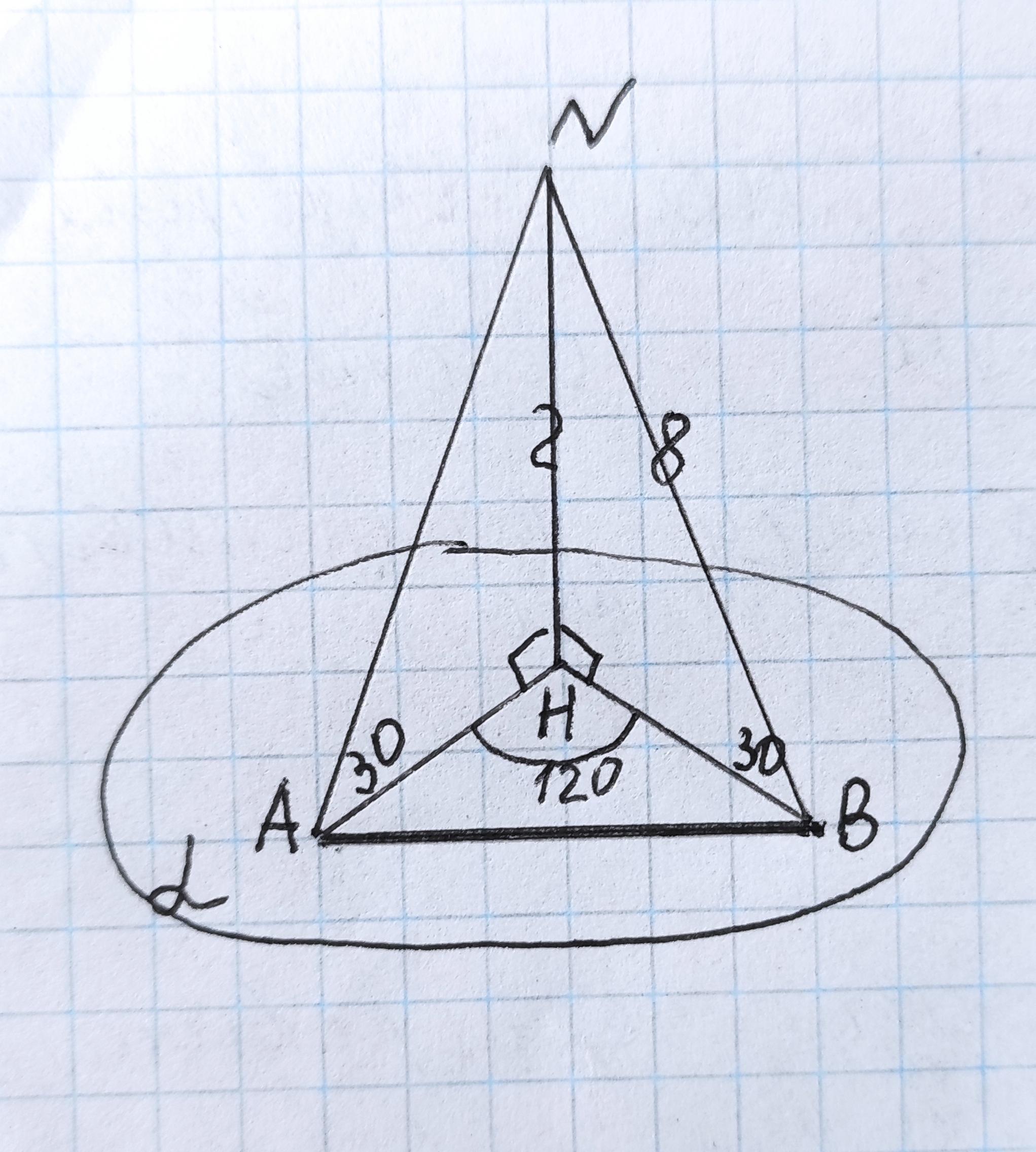
Із точки N до площини проведено похилі NА і NВ, які утворюють із даною площиною кути 30°. Кут між проекціями даних похилих на площину дорівнює 120°. Знайдіть відстань між основами похилих, якщо
NВ = 8 см.
dima1242004124:
ПЖ
Ответы
Ответ дал:
6
Из точки N к плоскости проведем две наклонные NA и NB ,перпендикуляр NH По условию ∠ NAH=∠NBH=30° =>
∠ АNН=∠ВNH=90°-30° =60° . Тк треугольники NAH и NBH равны по катету HN -общий и двум прилежащим углам,то AH= BH=8: cos30°=16/√3 (см).
ΔАВН , ∠АHВ=120°. По т. косинусов
АВ²=2НВ²(1-соs 120°)=2*256/3*(1+1/2)=256
АВ=16 см
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад