Question

Равносторонний треугольник со стороной 2 3 вращается вокруг своей высоты. Найти объём полученной фигуры. (Число Пи считать равным 3)

Answer 1

Ответ:

3

Объяснение:

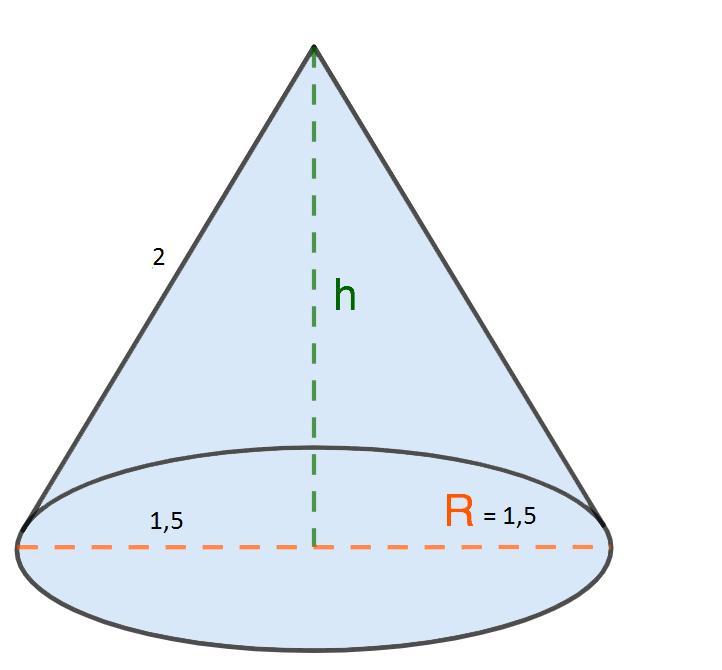
вращаясь вокруг своей оси треугольник образует фигуру конуса.

следовательно нам требуется найти объем полученного конуса.

формула объема конуса выглядит следующим образом:

$V = \frac{1}{3} * h * \pi * R^2$

$\pi *R^2$ в данной формуле, это площадь круга (S) который образуется при вращении треугольника.

h - это высота, которую нам требуется найти, для решения задачи.

найдём высоту по теореме Пифагора, т.к. высота в данном треугольнике образует два равных прямоугольных треугольника.

$h^2 = 2^2 - 1,5^2 =1,75\\h = \sqrt{1,75}$

радиус образованного от вращения треугольника круга будет равняться половине основания треугольника:

R = 1,5

считаем объем конуса:

$V = \frac{1}{3} * \sqrt{1,75} * 3 * 1,5^2 = 3$