Ответы
Ответ дал:
1
Решение задания прилагаю
Приложения:
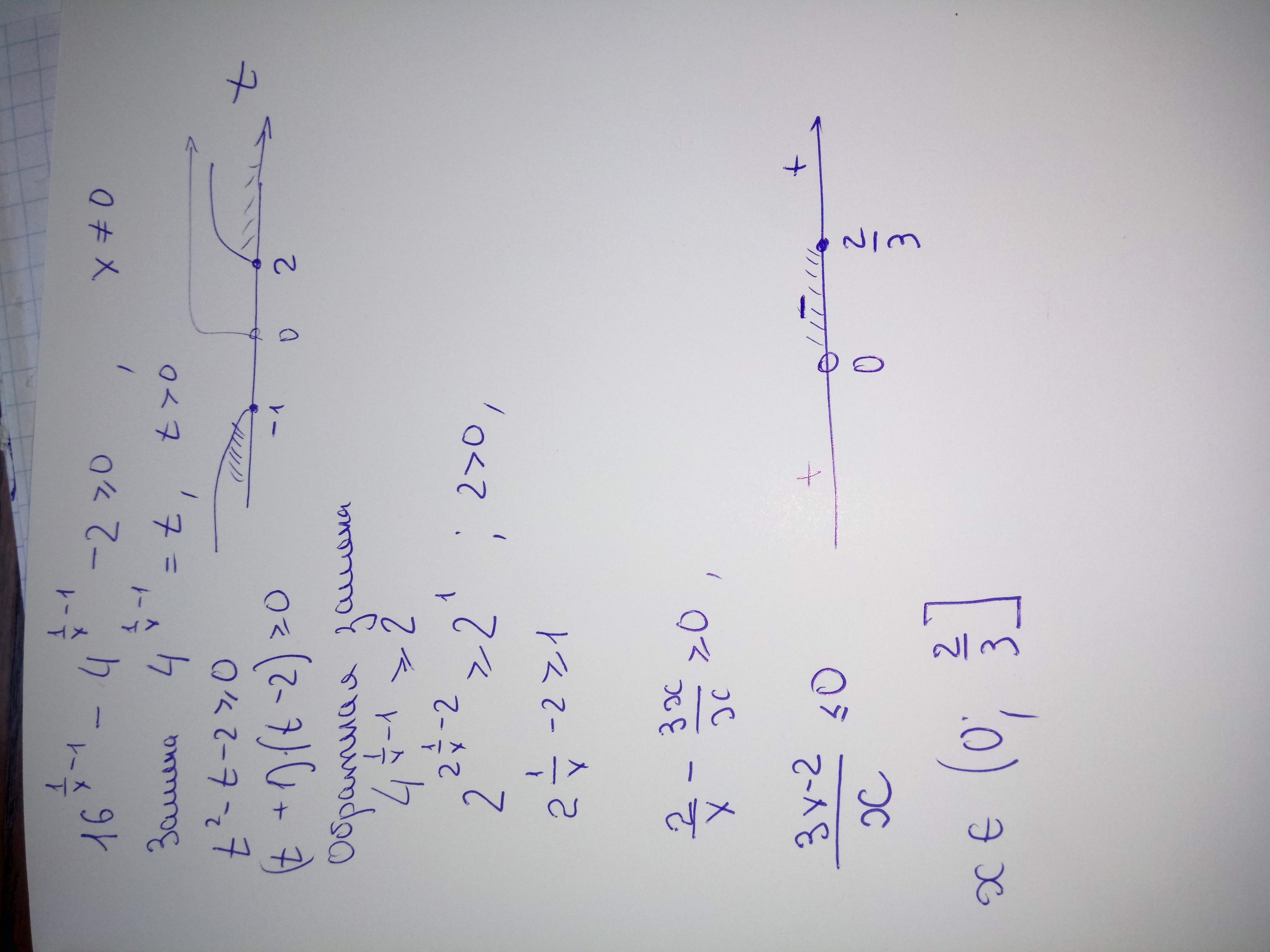
Ответ дал:
2
Пусть
(интервалы прикрепил к решению)
t ∈ ( -∞ ; -1] ∪ [2 ; ∞)
∈ ( -∞ ; -1] ∪ [2 ; ∞)
, поэтому первый интервал мы можем отбросить.
∈ [2 ; ∞)
Определим промежуток для x:
так как в степени стоит дробь с знаменателем с переменной, она будет возрастать при уменьшении переменной, значит
x ∈ (0 ; ]
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
10 лет назад
10 лет назад
