Question

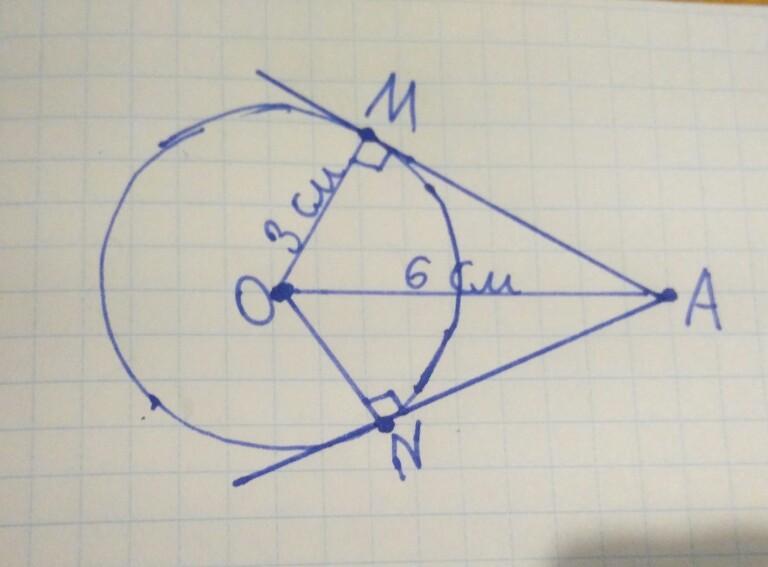
Рассчитайте по данным чертежа:
а) длины касательных участков MA и NA (с точностью до 0,1 см).
б) величина угла MAN.

Answer 1

Ответ:

а) МА = 5,2 см, NA = 5,2 см;

б) ∠МАN = 60°.

Пошаговое объяснение:

1) В прямоугольном треугольнике АМО катет ОМ равен 1/2 гипотенузы ОА, следовательно, ∠МАО = 30° (катет, лежащий против угла 30°, равен половине гипотенузы; верно и обратное утверждение).

2) ОN = ОМ - как радиусы одной и той же окружности; следовательно, ОN = 3 cм, а ∠ОАN = 30°.

3) ∠МАN = ∠МАО  + ∠ОАN = 30° + 30° = 60°.

∠МАN = 60°.  

4) Так как катет и гипотенуза прямоугольного треугольника АМО  равны катету и гипотенузе прямоугольного треугольника АNО, то, согласно четвёртому признаку равенства прямоугольных треугольников, эти треугольники равны.  Следовательно, МА = NА. (касательные, проведённые к данной окружности из одной и той же точки, равны).

5) Катет МА равен произведение гипотенузы ОА на косинус угла, прилежащего к этому катету:

МА = ОА · cos ∠МАО = 6 · cos 30° = 6 · √3 /2 = 3√3 cм ≈ 3 · 1,732 ≈ 5,196 ≈ 5,2 см

МА = 5,2см

А так как МА = NA, то NA ≈ 5,2 см  

NА = 5,2см

Ответ:  а) МА = 5,2 см, NA = 5,2 см; б) ∠МАN = 60°.