Question

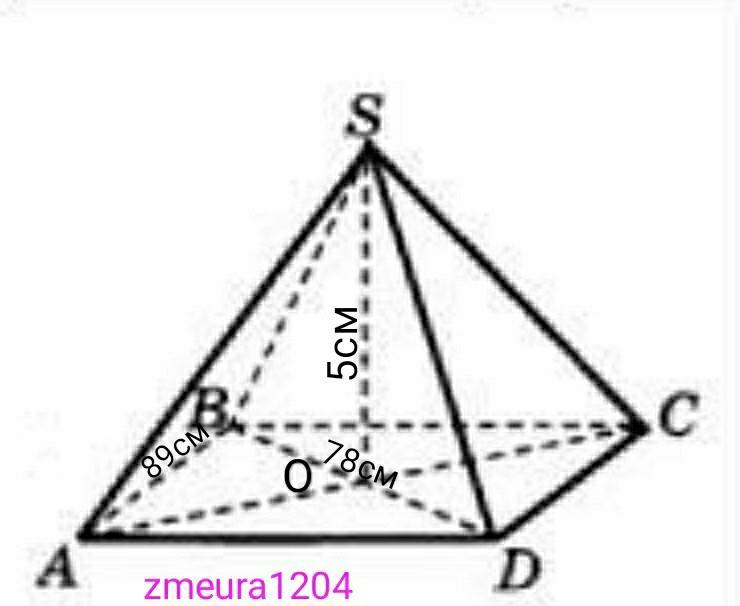
Вычислите объём прямой четырёхугольной пирамиды высотой 5 см, в основании которой лежит ромб со стороной 89 см и длиной одной из диагоналей 78 см.

Answer 1

Ответ:

V=10400см³

Объяснение:

Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.

ВО=ВD/2=78/2=39см.

∆АОВ- прямоугольный треугольник.

По теореме Пифагора

АО=√(АВ²-ВО²)=√(89²-39²)=

=√(7921-1521)=√6400=80см.

АС=2*АО=2*80=160см.

S(ABCD)=½*BD*AC=½*160*78=6240 см²

V=⅓*S(ABCD)*SO=⅓*6240*5=10400см³