Угол при вершине осевого сечения конуса равен 90 градусов. Найдите объем конуса, если его радиус равен 7 см
Аноним:
Уже комментировала эту задачу
Да? Тогда не решаю.
Вы осень быстро решаете. Я иногда даже удивляюсь. У меня на телефоне так не получается. Так что решите.
Не осень А ОЧЕНЬ
Не всегда, когда нужно создать чертеж, на это уходит время.
Ответы
Ответ дал:
0
Ответ:
343π/3 см³
Объяснение:
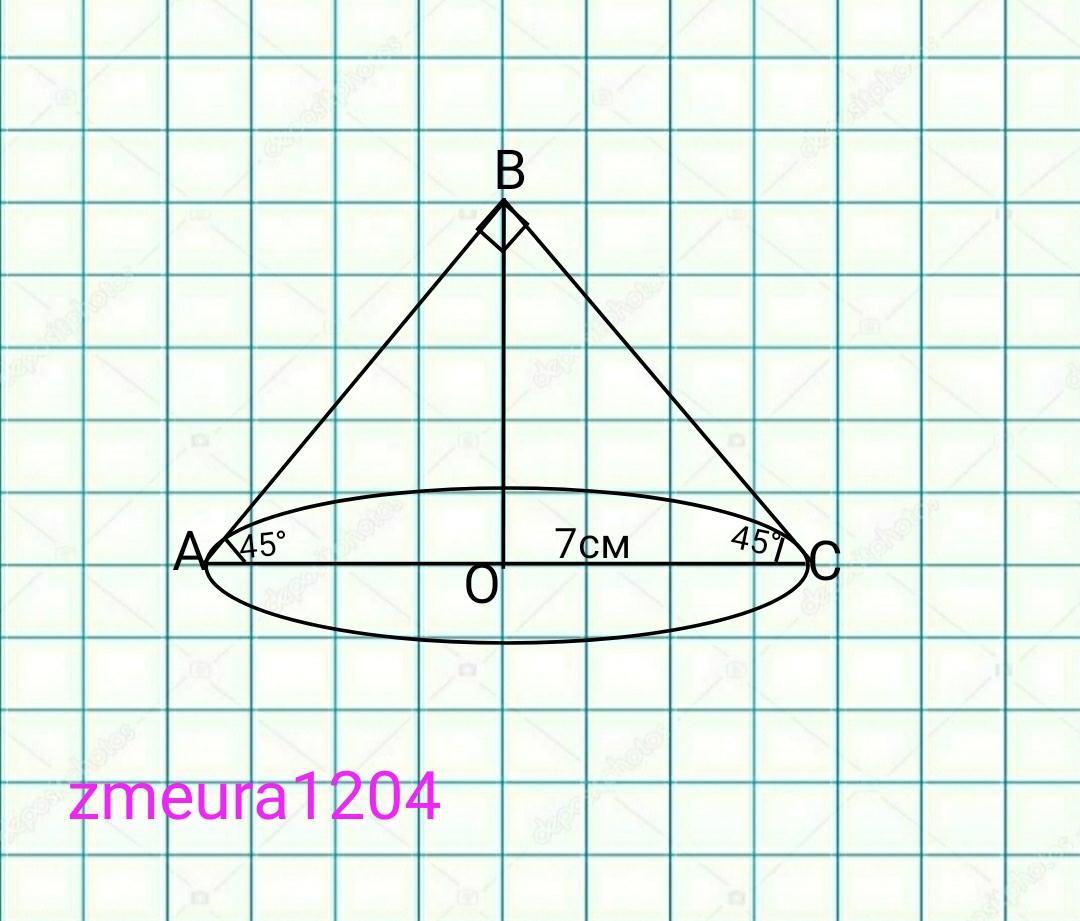
Так как угол при вершине 90°, треугольник ∆АВС осевого сечения прямоугольный равнобедренный треугольник.
ВО- высота и медиана прямоугольного треугольника.
Медиана прямоугольного треугольника равна половине гипотенузы.
ВО=½*АС
ВО=ОС=R.
V=⅓*Sосн*h=⅓*OC²*π*BO=⅓*7²*7π=
=343π/3 см³
Zmeura1204.
Приложения:
Вас заинтересует
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад