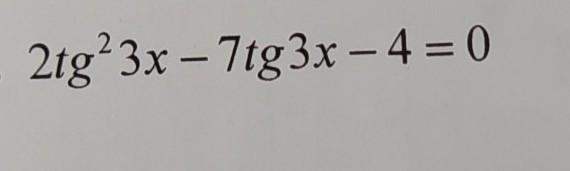Ответы
Ответ дал:
0
Ответ:
,
, n∈Z
Пошаговое объяснение:
Пусть tg(3x) = t,тогда
Вернёмся к замене:
а)
, n∈Z
б)
, n∈Z
Аноним:
помогите пожалуйста
Ответ дал:
0
решение квадратного уравнения
прикрепляю на фото
решаем через замену переменной
Приложения:

Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад