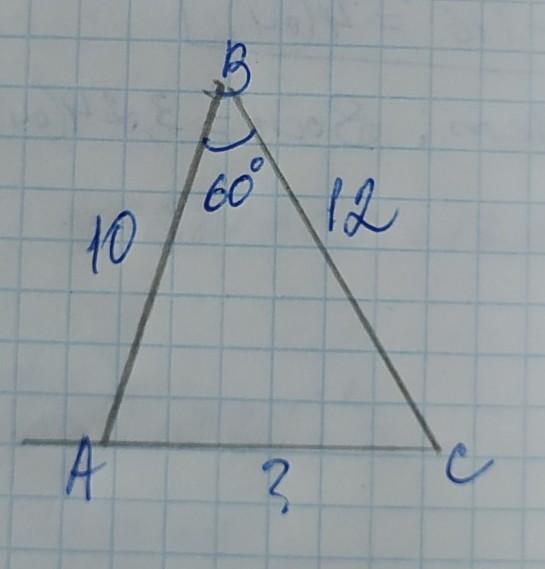
Дві сторони трикутника дорівнюють 12 см і 10 см. Знайти третю сторону, якщо кут між ними дорівнює 60°
Ответы
Ответ дал:
4
Ответ: АС=2√31
Объяснение:
Теорема косинусов:
АС^2=АВ^2+ВС^2-2*АВ*ВС*cos60°.
АС^2=12^2+10^2-2*12*10*0,5=124
АС=2√31
Ответ дал:
4
Ответ:
АС=2√31см
Объяснение:
Обозначим вершины треугольника А В С, АВ=10см, ВС=12см, и угломВ=60° между ними.
Используем теорему косинусов:
АС²=АВ²+ВС²–2×AB×BC×cosB=
=10²+12²–2×10×12×cos60°=
=100+144–240×1/2=244–240/2
=244–120=124
АС=2√31см
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад