При каком значении параметра a уравнение будет иметь один корень?
ax^3-x^2+1=0
antonovm:
a > (2корня из 3 )/9 или a < - (2корня из 3 )/9 , рассмотрите 3 случая : а = 0 ; a >0 ; a < 0 для второго и третьего случая используйте производную ( там всё будет зависеть от точки минимума ) ну и ещё , что в нуле левая часть равна 1 и кубическое уравнение всегда имееет хотя бы один действительный корень
Ответы
Ответ дал:
2
Ответ:
Объяснение:
ax³-x²+1=0
коэффициенты кубического уравнения
a, b=-1, c=0, d=1
дискриминант кубического уравнения
Δ=-4b³*d+bc²-4ac³+18abcd-27a²d²=-4b³*d-27a²d²=4-27a²
при Δ<0 уравнение имеет один вещественный и два комплексных корня
4-27a²<0
27a²>4
a²>4/27
если a²=4/27 то a=±√(4/27)=±2/(3√3)
тогда
a∈(-∞;-2/(3√3))∪(2/(3√3);+∞)
Ответ дал:
3
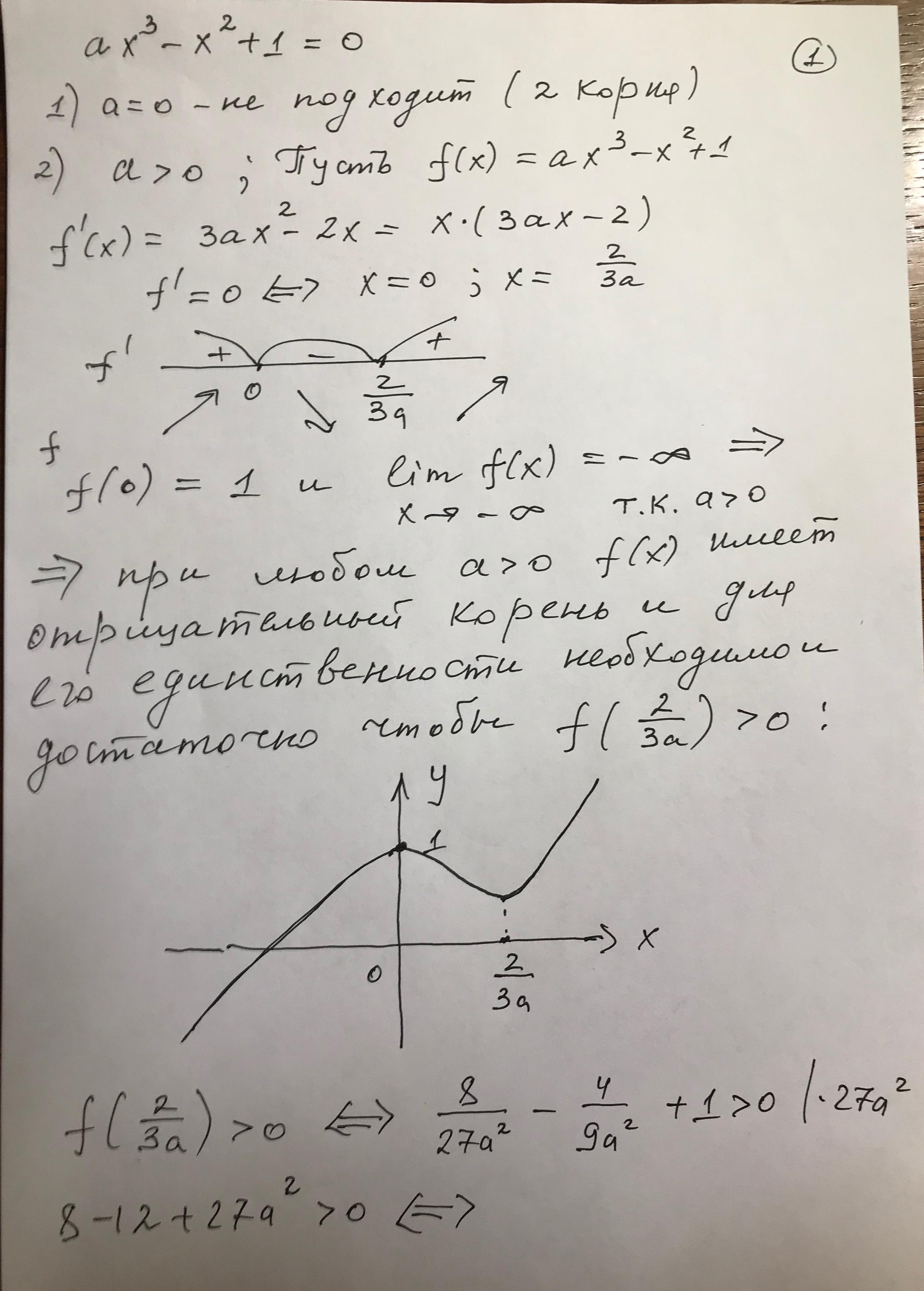
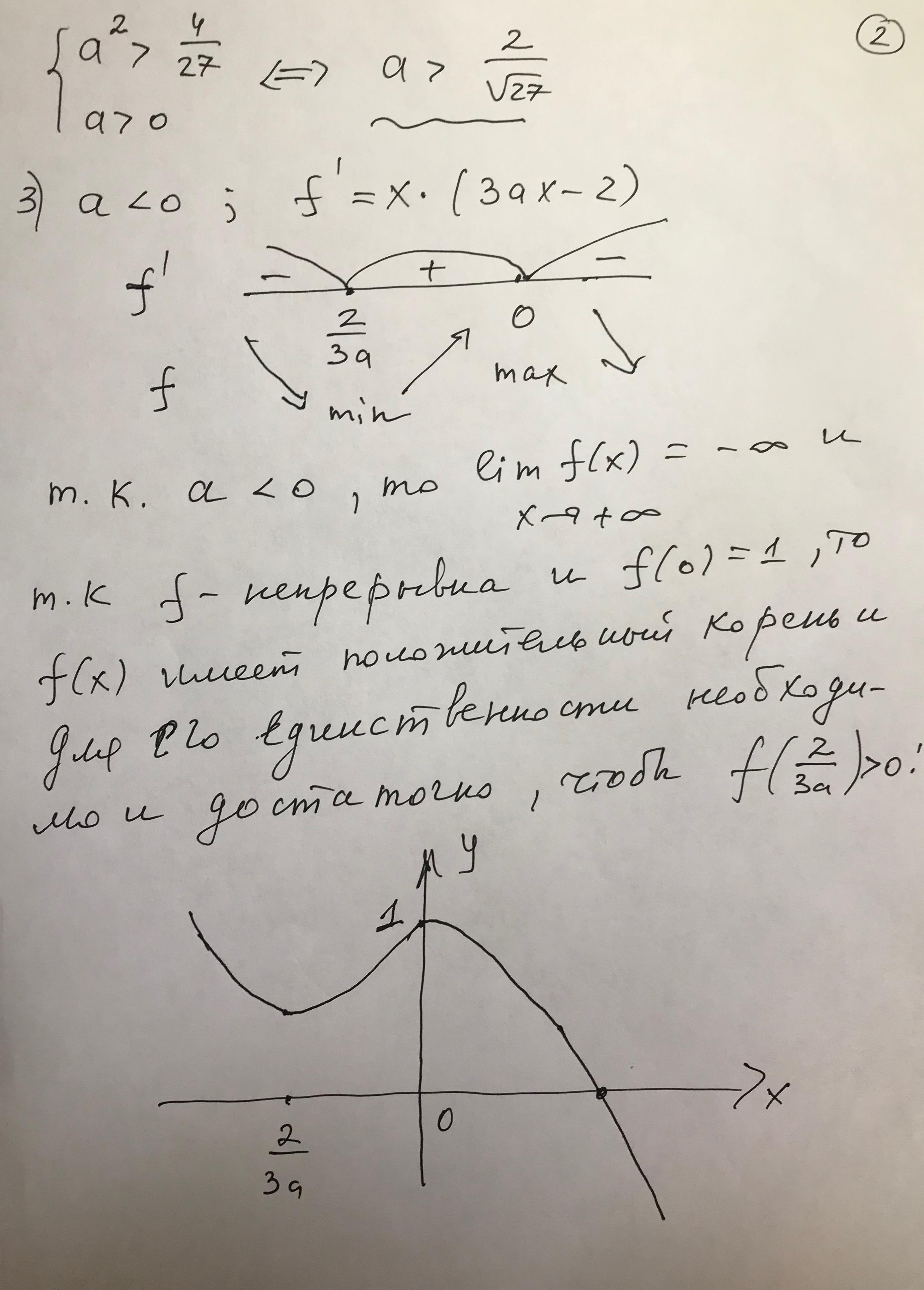
Решение : //////////////////////////////////
Приложения:
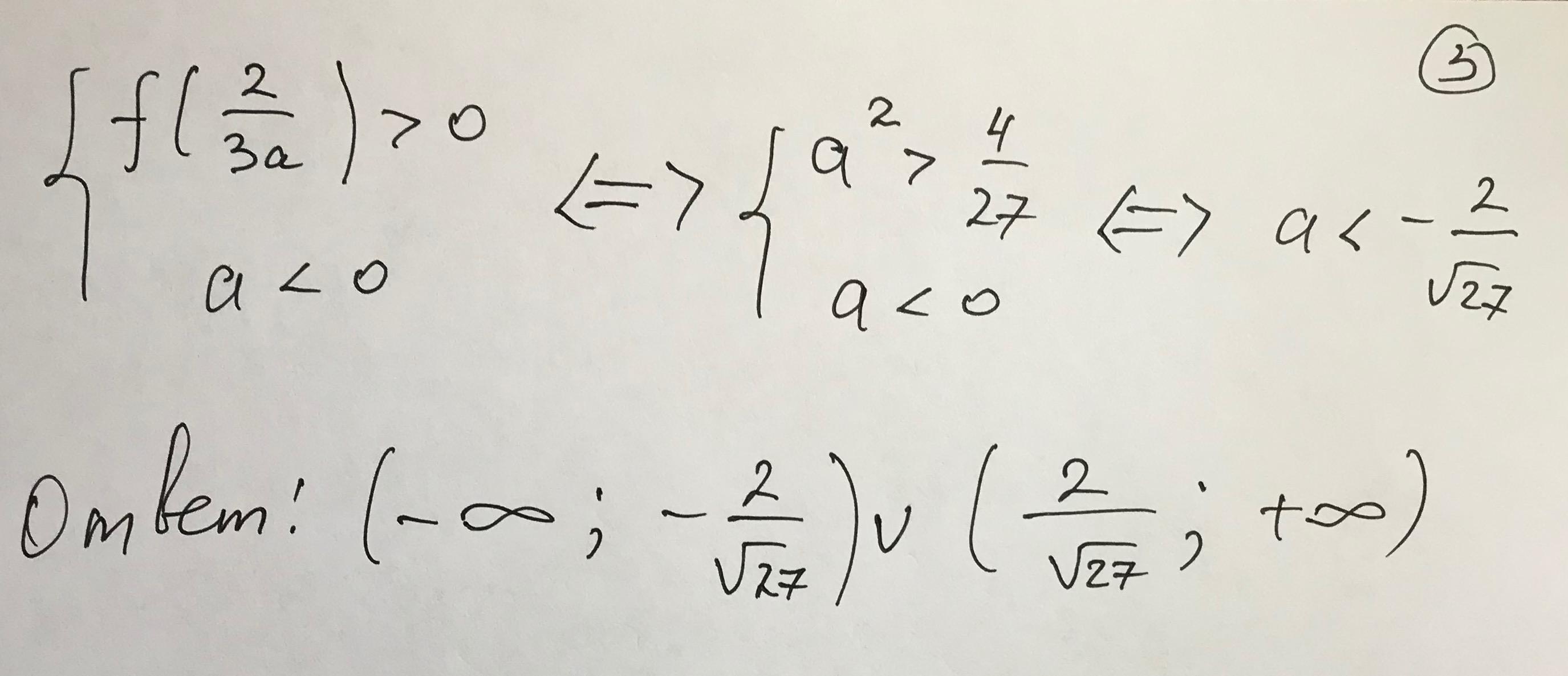
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад