Question

Вычислить площадь фигуры, ограниченной графиком функций y^2=8x и x=13

p.s. в основном, проблема с нахождением a и b для интеграла. Если решите полностью, буду очень благодарен

Answer 1

Ответ:

$y^2=8x$  -  парабола, симметричная оси ОХ ,

$x=13$  - прямая, параллельная оси ОУ .

Точки пересечения:  

$\left\{\begin{array}{lll}y^2=8x\\x=13\end{array}\right\ \ \left\{\begin{array}{lll}y^2=8\cdot 13\\x=13\end{array}\right\ \ \left\{\begin{array}{lll}y^2=104\\x=13\end{array}\right\ \ \left\{\begin{array}{lll}y=\pm \sqrt{104}\\x=13\end{array}\right$

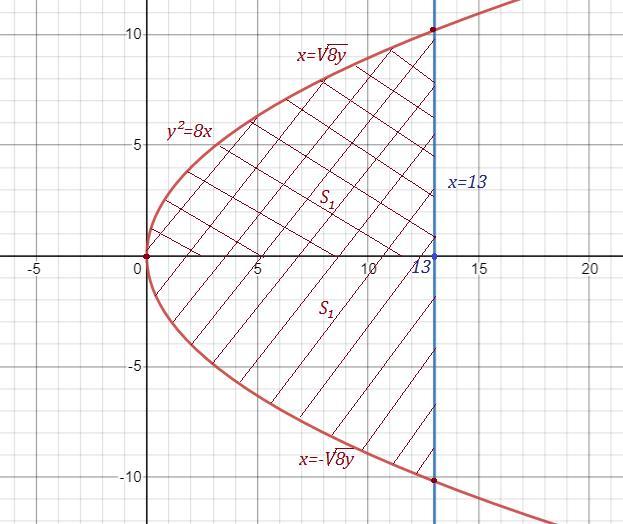
В этом примере нам в принципе не понадобятся точки пересечения. При интегрировании по "х" , ясно, что "х" изменяется от 0 до 13 . Смотри рисунок .

Выразим "у" через "х" . Получим уравнение двух ветвей параболы.

$y^2=8x\ \ \ \Rightarrow \ \ y=\pm \sqrt{8x}$  . Верхняя ветвь со знаком плюс, нижняя со знаком минус .

Воспользуемся симметричностью параболы относительно оси ОХ. Найдём площадь верхней области и удвоим её .

$\displaystyle S=2S_1=2\int\limits^{13}_0\, \sqrt{8x}\, dx=2\cdot \frac{(8x)^{\frac{3}{2}}}{8\cdot \frac{3}{2}}\Big|_0^{13}=\frac{1}{6}\cdot \sqrt{(8x)^3}\Big|_0^{13}=\frac{1}{6}\cdot (\sqrt{(8\cdot 13)^3}-0)=\\\\\\=\frac{1}{6}\cdot \sqrt{8^{3}\cdot 13^{3}}=\frac{1}{6}\cdot 8\cdot 13\cdot \sqrt{8\cdot 13}=\frac{1}{6}\cdot 8\cdot 13\cdot 2\cdot \sqrt{2\cdot 13}=\frac{104}{3}\cdot \sqrt{26}$