Сторона основания правильной треугольной пирамиды равна 4 см, а её боковое ребро 2√3см. Вычислите объём пирамиды.
Прошу помогите!!!!
Ответы
Відповідь:
Покрокове пояснення:
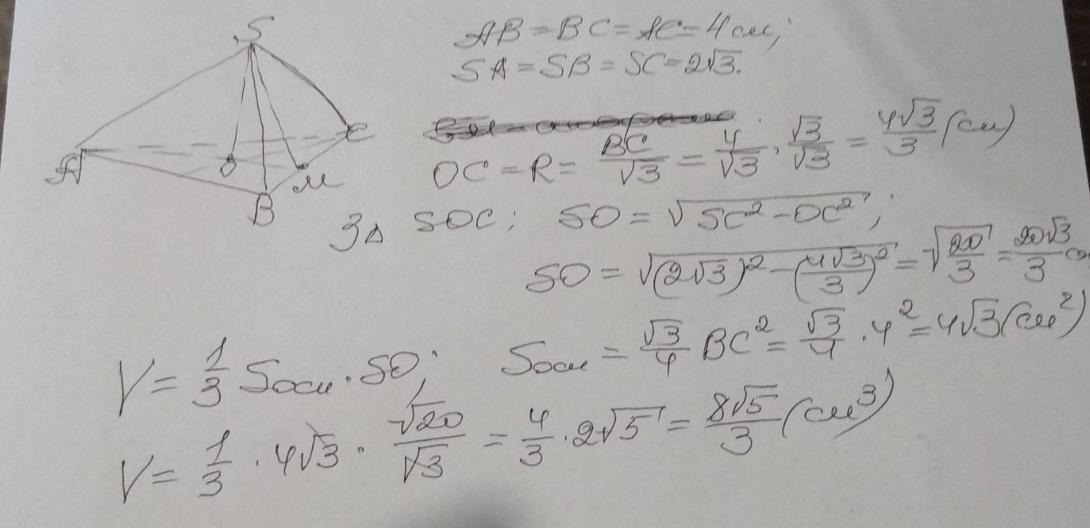
Ответ:
V = (8√5)/3
Пошаговое объяснение:
Объем пирамиды вычисляется по формуле:
V = (1/3) * S * H ,
где S - площадь основания, H - высота пирамиды.
Пирамида правильная, следовательно, в ее основании лежит правильный ( т.е. равносторонний ) треугольник. Площадь равностороннего треугольника ( или, площадь основания данной пирамиды ) со стороной 4 равна:
SΔ = (a²*√3) / 4 = ( 4²*√3 ) / 4 = 4√3
Радиус окружности, описанной около основания пирамида равна:
R = (2/3)*h = (2/3)*(a√3/2) = (1/√3) *4 = 4/√3
Боковое ребро, высота пирамиды и радиус описанной около основания ( правильного треугольника ) {пирамиды} окружности связаны теоремой пифагора ( потому что составляют прямоугольный треугольник, при чем боковое ребро пирамиды лежит против прямого угла ). Значит, можно вычислить высоту пирамиды:
H = √(L²-R²) = √(2√3)²-(4/√3)² = √(12 - 16/3 ) =√(20/3) = 2√(5/3)
V = (1/3) * (4√3) * (2√(5/3)) = 8√5/3