1. найдите длины сторон треугольника ADC,если A(3,-1,3) B(3,-2,2) C(2,2,3) D(2,2,2)
2. найти интеграл
даю 25 баллов, помогите
Приложения:
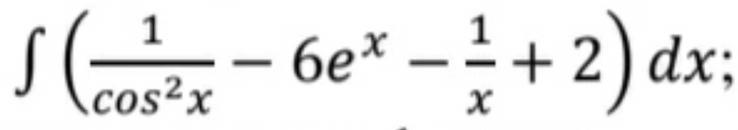
Ответы
Ответ дал:
0
Ответ:
1) 1, √10 и √11
2) tg x - 6e^x - ln|x| + 2x + C
Пошаговое объяснение:
1. Длину отрезка с концами в точках (x_1; y_1; z_1) и (x_2; y_2; z_2) можно найти по формуле
Найдем длины сторон AD, AC и DC:
2.
Вас заинтересует
3 года назад
3 года назад
9 лет назад