Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
сначала вычислим неопределенный интеграл
внесем cosx под знак дифференциала
∫(cosx/(3+2sinx))dx=-∫(1/(3+2sinx))dsinx=
умножим и разделим на 2
=-(1/2)∫(1/(3+2sinx))d(2sinx)=
под знаком дифференциала прибавим 3
=-(1/2)∫(1/(3+2sinx))d(3+2sinx)=
заменим переменную 3+2sinx=y
=-(1/2)∫(1/y)dy=
это табличный интеграл
=-(1/2)lnIyI+c
вернемся к x
=-(1/2)lnI3+3sinxI+c
вычислим определенный интеграл
п/2 п/2
∫(cosx/(3+2sinx))dx= (-(1/2)lnI3+2sinxI)=-(1/2)(lnI3+2sin(п/2)I-lnI3+2sin(п/4)I)
п/4 п/4
=-(1/2)(lnI3+2I-lnI3+2((√2)/2)I)=-(1/2)(ln5-ln√2I)=-(1/2)ln(5/√2)
это решать несложно но там пределы интегрирования с корнями, очень сложные вычисления
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад
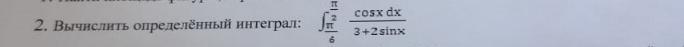
Y=-x^2+10x-16, y=2